Evaluación 1

• ¿En cuál de las siguientes operaciones el resultado es −2?

1. \(\frac{{3\, \times\, \left( { - 4} \right) \,\times\, 5 \,\times\, \left( { - 6} \right)}}{{9 \,\times\, \left( { - 5} \right) \,\times\, 4}}\)
2. \(\frac{{18 \,\times\, \left( { - 20} \right)}}{{\left( { - 5} \right) \,\times\, \left( { 36} \right)}}\)
3. \(\frac{{{{\left( { - 2} \right)}^4}}}{{\left( { - 2} \right) \,\times\, \left( { - 4} \right)}}\)
4. \(\frac{{30 \,\times\, 12}}{{ - 45 \,\times\, {{( - 2)}^2}}}\)

• ¿Cuánto es 5 × 5⁵?

1. 5⁵
2. 5⁶
3. 5²⁵
4. 25⁵

• ¿Cuánto es la mitad de 4²⁰¹⁴?

1. 2²⁰¹⁴
2. 4²⁰¹³
3. 4¹⁰⁰⁷
4. 2⁴⁰²⁷

• ¿A qué potencia debemos elevar 4⁴ para obtener 4¹²?

1. 2
2. 3
3. 4
4. 8

• Dos paralelas se cortan por transversales de modo que forman los ángulos que se muestran en la figura. ¿Cuánto mide el ángulo  x?


1. 50°
2. 90°
3. 75°
4. 65°

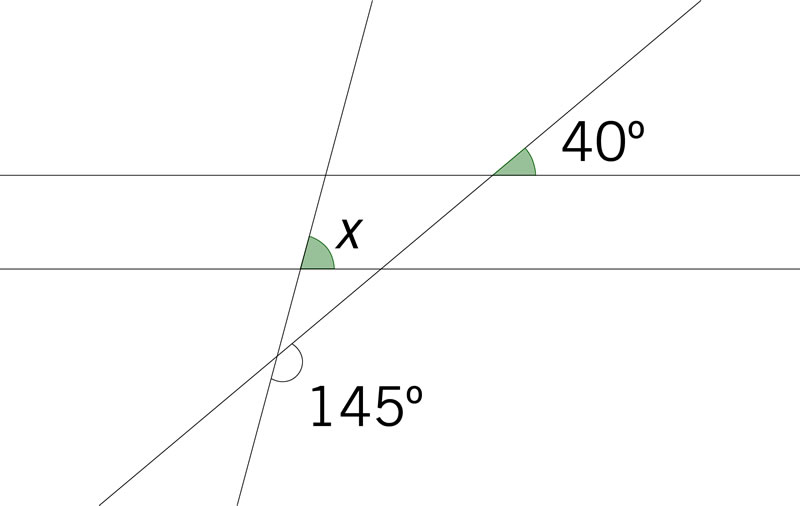
• ¿Cuánto suman los ángulos internos de un romboide cualquiera?

1. 180°
2. 360°
3. 540°
4. 720°

• En esta figura, el radio de los círculos grandes es de 2 cm y el de los pequeños, 1 cm. ¿Cuánto mide el área de la región sombreada?


1. 2π cm²
2. 4π cm²
3. 6π cm²
4. 8π cm²

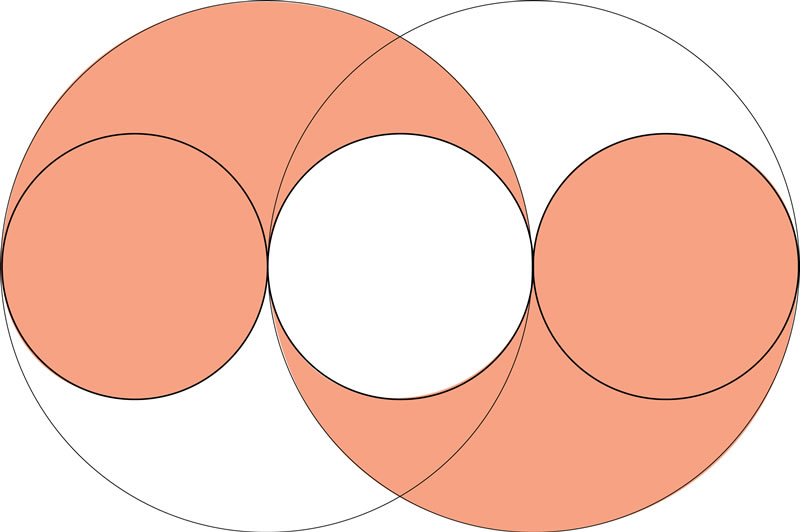
• A una reunión de padres de familia asisten 17 mujeres y 3 hombres. ¿Cuál es el porcentaje de hombres con respecto del total de padres de familia?

1. 3%
2. 15%
3. 16%
4. 17%

• Los círculos de la figura son todos iguales y su radio es igual a 1 cm. ¿Cuánto mide el área de la región en el centro?


1. 4π cm²
2. 2 − 3π cm²
3. 4 − 2π cm²
4. 4 − π cm²

• Las siguientes tríadas de números corresponden a las medidas, en centímetros, de tres segmentos rectos. ¿Con qué tríada no se puede construir un triángulo?

1. 3, 4, 5
2. 2, 3, 4
3. 3, 3, 3
4. 2, 3, 6

• Fabiola obtuvo un cupón de 20% de descuento para una conocida tienda de ropa. Si compró un pantalón cuyo precio original es de $100.00 y en la etiqueta indicaba un descuento de 30%, ¿cuánto pagó por la prenda si utilizó el cupón?

1. $56.00
2. $50.00
3. $44.00
4. $90.006

• De la esquina de un cubo de 1 m de arista se corta y extrae un cubo de 80 cm de arista. ¿Cuánto mide la superficie de la figura remanente que se muestra?


1. 4 m²
2. 5 m²
3. 6 m²
4. 7 m²

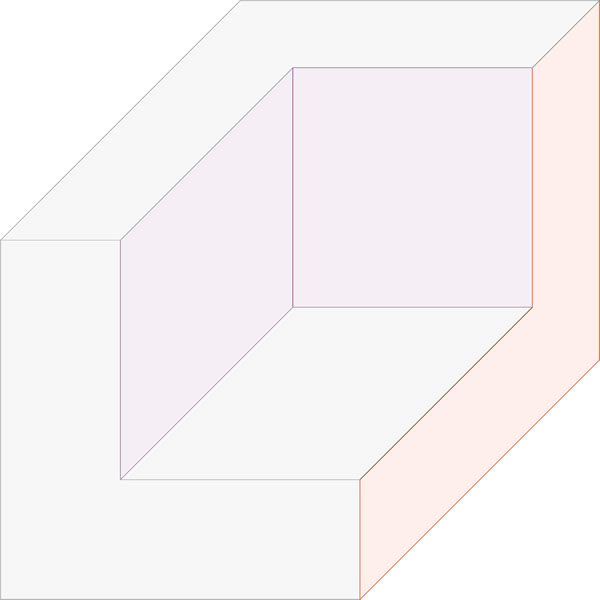
• En la promoción “La tómbola del descuento” de una tienda de autoservicio los clientes obtienen distintos descuentos por sus compras. Si Alma pagó $160.00 por un artículo cuyo precio original era de $200.00, ¿de cuánto fue el descuento que obtuvo en la tómbola?

1. 40%
2. 30%
3. 10%
4. 20%

• Un tinaco con 100 L de agua se deja abierto a la intemperie, y se observa que el líquido disminuye 5% cada día por efectos de la evaporación. ¿Qué cantidad de agua tendrá el tinaco en 3 días?

1. 90 L
2. 90.25 L
3. 85 L
4. 85.74 L

• Una población de bacterias se duplica cada minuto. Si cinco minutos después de iniciar el conteo hay 160 bacterias en la muestra, ¿de cuántas era la población inicial?

1. 5
2. 8
3. 10
4. 12

• En una caja hay dos canicas rojas y una negra. Si se extraen dos canicas al azar, ¿cuál de los siguientes eventos es más probable?

1. Las canicas extraídas son del mismo color.
2. Las canicas extraídas son de distinto color.
3. La canica que queda en la caja es negra.
4. Los eventos anteriores son igual de probables.

• Si simultáneamente se lanzan tres monedas, ¿cuál de los siguientes eventos es menos probable?

1. Las tres monedas muestran la misma cara.
2. Salen dos soles y un águila.
3. Salen dos águilas y un sol.
4. Salen tres soles.

• El promedio de las edades de tres hermanos es de 9 y su mediana es 8. ¿Cuál es la edad de los hermanos si el mayor tiene 11 años?

1. 7, 9, 11
2. 7, 8, 11
3. 8, 8, 11
4. 6, 10, 11

• Si A = {3, 2, 7, 6, 2} y B = {4, 6, 2, 8}, ¿cuál de las siguientes afirmaciones es falsa?

1. El promedio de A es menor al promedio de B.
2. La mediana de A es menor a la mediana de B.
3. La mediana de A es mayor a la mediana de B.
4. El promedio de A es menor a la mediana de B.

• ¿Cuál es el resultado de la operación  (-8)³ ÷ (−4)?

1. −6
2. 128
3. 6
4. −128

• ¿Cuál es el resultado de la operación  \(\frac{13^{3}\,\times\,13^{4}}{13^{5}}\)

1. 13⁶
2. 13⁴
3. 13^-6
4. 13^-4

• ¿Cuál es el resultado de la operación  \(9^{10}\,\times\,\frac{(9^{4})^{3}}{9^{12}}\,\times\,9^{-2}\) ?

1. 9⁸
2. 9¹²
3. 9^-4
4. 9^-3

• A la suma de los ángulos internos de un paralelogramo se le resta la suma de los ángulos internos de un triángulo escaleno. ¿Cuál es el resultado final?

1. 360°
2. 0°
3. 90°
4. 180°

• ¿Con cuál de las siguientes condiciones se puede construir un triángulo único?

1. Se conocen las longitudes de sus tres lados.
2. Dos de sus lados miden lo mismo y su suma es mayor que el tercer lado.
3. Se conoce la longitud de dos de sus lados.
4. Se conoce la medida de sus ángulos internos.

• ¿Cómo se calcula el área que ocupa la superficie de un prisma de base hexagonal?

1. Se obtiene el área del hexágono que forma la base y se multiplica por la altura del prisma.
2. Se obtiene el área del hexágono que forma la base y se multiplica por el área de la cara lateral del prisma.
3. Se obtiene el área de la cara lateral de prisma y se suma al área de la base.
4. Se obtiene el área de una cara lateral del prisma y se multiplica por seis. Al resultado se le suma dos veces el área de la base.

• La batería de una computadora portátil tiene el 12% de su capacidad total y 20 minutos después la computadora se apaga. ¿Cuántos minutosdura la batería con el 100% de carga?

1. 186.7 minutos
2. 146.7 minutos
3. 166.7 minutos
4. 144 minutos

• El día lunes cuatro personas vieron un video en Internet. El día siguiente el número de personas que vio el mismo video era de 89. ¿Cuál fue la tasa con la que aumentó la cantidad de personas que vio el video?

1. 2 225%
2. 22.25%
3. 4.5%
4. 45%

• En un puesto de una feria hay un estanque con siete patos de plástico, numerados del 1 al 7. Si con una caña de pescar se saca uno al azar, ¿cuál de los siguientes eventos es más probable que suceda?

1. Que el número del pato seleccionado sea impar.
2. Que el número del pato seleccionado sea par.
3. Que el número del pato seleccionado sea un múltiplo de 3.
4. Todos los eventos tienen la misma probabilidad de ocurrir.

• En un torneo de dominó los integrantes de dos equipos obtuvieron las siguientes puntuaciones: equipo 1: 12, 4, 3, 7, 3 ; equipo 2: 6, 14, 4, 10. ¿Cuál de ellos tuvo mejor desempeño?

1. Tuvieron el mismo desempeño, porque ambos sumaron la misma puntuación.
2. El equipo 2, porque su media aritmética es mayor que la del equipo 1.
3. El equipo 1, porque tiene más integrantes.
4. El equipo 2, porque hay menos diferencia entre los puntos de sus integrantes.

• Beatriz tiene m canicas, Luis tiene seis veces más que Beatriz y Carla tiene la mitad de las que tiene Luis. ¿Cuántas canicas tienen entre los tres?

1. 7m
2. 8m
3. 9m
4. 10m

• ¿Qué expresión representa el área de la superficie de este prisma rectangular?


1. 8x³
2. 48x²
3. 20x²
4. 48x³

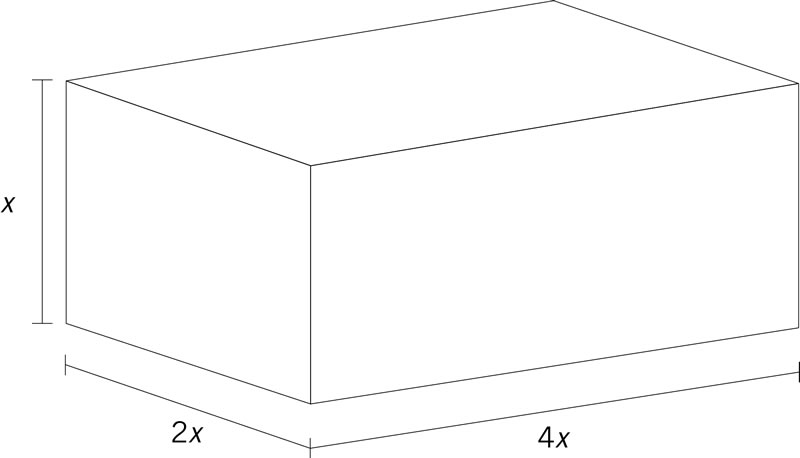
• Silvia tiene en su alcancía  p monedas de $10.00,  q de $5.00 y  r de $2.00. Su hermano tiene  q monedas de $10.00,  r de $5.00 y p de $1.00. Si juntan sus ahorros para comprar un regalo a su papá, ¿de cuánto dinero disponen?

1. 10p + 15q + 7r
2. 11p + 15q + 7r
3. 11p + 10q + 7r
4. 15p + 7q + 10r

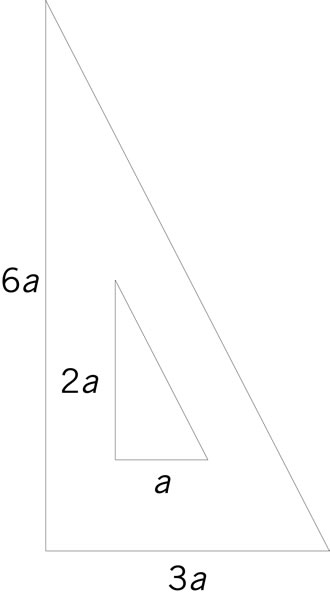
• De la parte central de un triángulo rectángulo de altura 6 a y base 3 a se extrae un triángulo rectángulo de altura 2 a y base a. ¿Cuál es el área de la figura resultante?


1. 8a²
2. 16a²
3. 6a²
4. 9a²

• Si en un cuadrado cuya área es  a² la base aumenta en 9 unidades y la altura disminuye en 3, ¿cuál será el perímetro de la figura resultante?

1. 4a² + 12
2. 4a + 12
3. 2a² + 6
4. 2a + 6

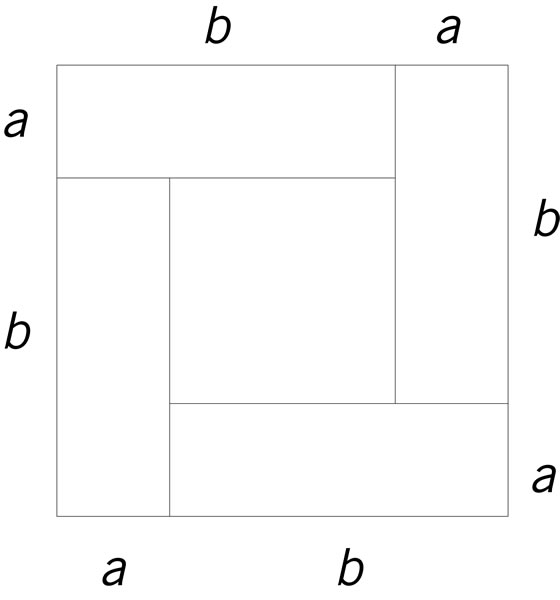
• ¿Cuál de las siguientes equivalencias representa la relación entre el cuadrado mayor y el cuadrado interno y los rectángulos que lo componen?


1. \({\left( {b + a} \right)^2} = {\left( {b - a} \right)^2} + 4ab\)
2. \({\left( {b + a} \right)^2} = {\left( {b - 2a} \right)^2} + 4ab\)
3. \({\left( {b + a} \right)^2} = {b^2} + 2ab + {a^2}\)
4. \({\left( {b + a} \right)^2} = {b^2} + 4ab\)

• ¿Cuál es el resultado de la operación   \(34x\,+\,20x\,+\,4x\, \,–\,54x\)?

1. \(4x\)
2. \(4 \)
3. \(–4x\)
4. \(–4\)

• ¿Cuál es el resultado de la operación   \(–89x +\frac{113}{4} x + \frac{70}{8}x\)?

1. \(–52 \)
2. \(–52x \)
3. \(–10x \)
4. \(–61x\)

• ¿Cuál es la expresión que falta para que se cumpla la igualdad   \(3mn + 2m^2\) ____ \(+ \,13mn \,+ 7m^2 = 16mn + 4m^2\)?

1. \(+\,5m^2\)
2. \(+\,5mn \)
3. \(–\,5m^2\)
4. \(–\,5mn\)

• ¿Cuál es el resultado de la operación  \(36ab\,+\,4c^2\,+\,8ab\,+\,(7c)^2\,–\, \,45ab\ \,–\,17c^2\)?

1. \(–ab\,+\,4c^2 \,–\,10c \)
2. \(ab\,+\,10c^2\)
3. \(–ab\,+\,36c^2\)
4. \(–ab\, \,–\,10c^2\)

• ¿Cuál de las siguientes expresiones es equivalente a   \(5z^2(3w + 4)\)?

1. \(15zw^2 + 20 \)
2. \(15zw + 20z \)
3. \(15w + 20\)
4. \(15z^2w + 20z^2\)

• ¿Cuál de las siguientes expresiones no es equivalente a   \(8ab\,+\,2b^2 \,– \, 16b^3\)?

1. \(b(8a + 2b \,–\, 8b^2)\)
2. \(2b(4a + b \,–\, 8b^2)\)
3. \(8(ab + b \,\,\, –\, 2b^2)\)
4. \(–2b(–4a \,– b + \, 8b^2)\)

Evaluación 2

• Un prisma de base cuadrangular y un cubo tienen un volumen de 8 m³. Si el prisma tiene una base igual a la cuarta parte de la base del cubo, ¿cuánto mide su altura?

1. 2 m
2. 4 m
3. 6 m
4. 8 m

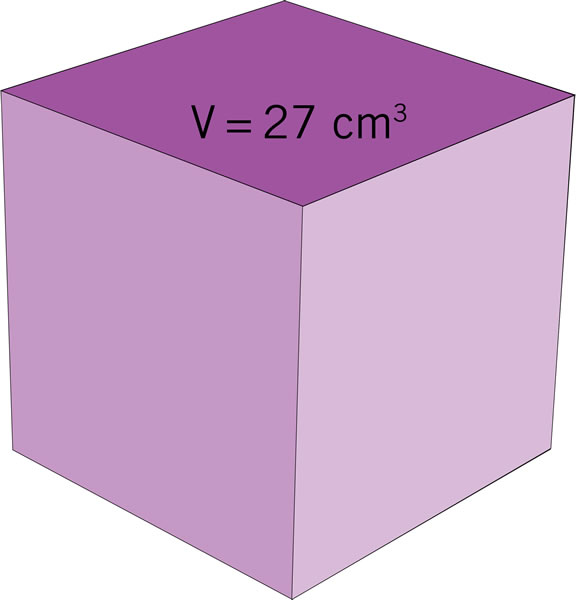
• El volumen del cubo es de 27 cm³. Calcula el área total de sus caras laterales.


1. 54 cm²
2. 27 cm²
3. 90 cm²
4. 9 cm²

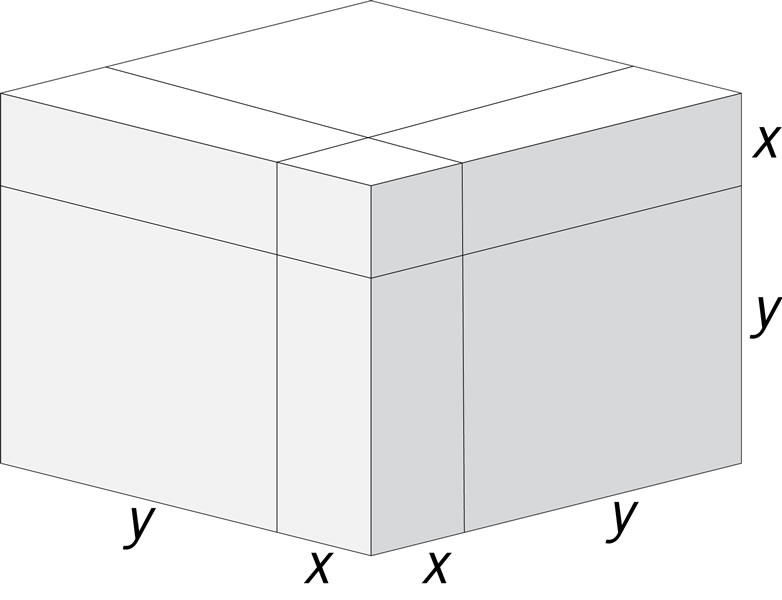
• Un cubo se corta siguiendo las líneas que muestra la figura. ¿Cuál de las equivalencias se deduce de esta descomposición de volumen?


1. \({\left( {x + y} \right)^3} = 6\left( {{x^2} + 2xy + {y^2}} \right)\)
2. \({\left( {x + y} \right)^3} = {x^3} + 3{x^2}y + 3x{y^2} + {y^3}\)
3. \({\left( {x + y} \right)^3} = {x^3} + 3{x^2}y + 3x{y^2}\)
4. \({\left( {x + y} \right)^3} = {x^3} + {y^3} + 6{x^2}y + 6x{y^2}\)

• P y Q son dos prismas de bases iguales. Si el volumen de P es el triple del volumen de Q, ¿cómo es la altura de P en relación con la altura de  Q?

1. Ambas alturas son iguales.
2. La altura de P es la tercera parte de la altura de Q.
3. La altura de P es el triple de la altura de Q.
4. La altura de P es la mitad de la altura de Q.

• Si se quiere dividir un prisma de altura  h en dos piezas de igual volumen con un corte paralelo a su base, ¿a qué distancia de la base se debe realizar el corte?

1. \(\frac{1}{3}h\)
2. \(\frac{1}{2}V\)
3. \(\frac{1}{2}h\)
4. \(\frac{2}{3}h\)

• P y Q son pirámides de igual volumen. Si la altura de  P se duplica y el área de la base de  Q también se duplica, dejando igual las demás medidas, ¿qué relación se satisface entre los volúmenes de   P y  Q ahora?

1. El volumen de P es menor que el volumen de  Q.
2. El volumen de P es mayor que el volumen de  Q.
3. El volumen de P es igual al volumen de  Q.
4. No se puede saber.

• Una pirámide y un cubo tienen bases y volúmenes iguales. Si la arista del cubo mide  a unidades, ¿cuánto mide la altura de la pirámide?

1. \(\frac{1}{3}a\)
2. \(a\)
3. \(2a\)
4. \(3a\)

• ¿Cuál de las siguientes opciones no muestra (en centímetros) las medidas de la base de un prisma rectangular de 240 cm³ de volumen y 10 cm de altura?

1. 3 y 8
2. 24 y 10
3. 6 y 4
4. 12 y 2

• Para cierto trayecto el viaje en taxi cuesta $120.00. A un pasajero que no quería gastar tanto, el taxista le propone esperar a otras personas con el mismo destino y dividir el gasto. El taxi puede transportar 4 pasajeros, pero cuando había apenas 3, ninguno quiso esperar más e iniciaron el viaje. ¿Cuánto más pudo haberse ahorrado cada pasajero si hubiesen esperado a una cuarta persona?

1. $40.00
2. $30.00
3. $20.00
4. $10.00

• En una secundaria se forman 15 filas de 12 estudiantes para hacer honores a la bandera. ¿Cuántas filas habría si cada una fuera de 9 estudiantes?

1. 8
2. 18
3. 20
4. 12

• Al considerar un volumen fijo, la relación entre el área de la base y la altura de una pirámide es una relación de proporcionalidad:

1. directa.
2. cuadrática.
3. inversa.
4. variable.

• Al lanzar 10 volados se obtuvieron los resultados que muestra la tabla. ¿Cuál de las relaciones siguientes se cumple para el evento "Sale águila"?

Volado	1	2	3	4	5	6	7	8	9	10
Resultado	sol	águila	águila	sol	sol	sol	águila	sol	sol	águila

1. Su probabilidad teórica fue mayor a su probabilidad frecuencial.
2. Su probabilidad teórica fue menor a su probabilidad frecuencial.
3. Su probabilidad teórica fue igual a su probabilidad frecuencial.
4. Ninguna de las anteriores.

• Si 10 decoradores requieren 12 días en cubrir con papel tapiz una superficie de 200 m², ¿cuánto tiempo tardarán 30 decoradores en cubrir esa misma superficie? Supón que todos trabajan al mismo ritmo.

1. 3 días.
2. 4 días.
3. 12 días.
4. 36 días.

• De una urna con pelotas de tres colores distintos se realizaron 30 extracciones al azar y después de cada extracción la pelota se regresó a la urna. Los resultados fueron los siguientes: 20 veces las pelotas fueron rojas, 5 azules y 5 verdes. ¿Cuál es la probabilidad frecuencial de obtener una pelota roja?

1. \(0.2\)
2. \(\frac{2}{3}\)
3. \(\frac{{30}}{{20}}\)
4. \(\frac{1}{3}\)

• En principio, para cualquier evento en particular si un experimento aleatorio se repite un número de veces cada vez mayor, ¿cuál de las siguientes afirmaciones es correcta?

1. Su probabilidad frecuencial es menor a su probabilidad teórica.
2. Su probabilidad frecuencial es mayor a su probabilidad teórica.
3. Su probabilidad frecuencial es igual a su probabilidad teórica.
4. Su probabilidad frecuencial tiende a ser igual a su probabilidad teórica.

• El volumen de un prisma cuadrangular de 16 cm de altura, es de 144 cm³. ¿Cuánto mide cada lado de la base?

1. 8
2. 4
3. 9
4. 3

• Manuel tarda 30 minutos en llegar de su casa a la escuela caminando con una rapidez promedio de 5 km/h. Si en bicicleta su rapidez promedio es de 20 km/h, ¿cuánto tiempo se tardará en el mismo trayecto?

1. 7.5 minutos
2. 15 minutos
3. 120 minutos
4. 10 minutos

• Una cisterna cúbica de 2.5 m de arista contenía una cuarta parte de su capacidad. Si una pipa de agua la llenó por completo, ¿qué cantidad agregó a la cisterna?

1. 15.6 m³
2. 4.7 m³
3. 11.7 m³
4. 3.9 m³

• Un dado cúbico tiene en sus caras los números 1, 2, 2, 4, 5 y 6. ¿Cuál es la probabilidad teórica de que al lanzarlo la cara que caiga hacia arriba sea un múltiplo de dos?

1. 0.5
2. 4
3. 0.33
4. 0.67

• Debido a un error tipográfico, en un libro de texto se lee la siguiente expresión: \[\frac{1}{2}\sqrt {5 + 4 \times 10 - 6} = 3\]
         ¿Cuál de las siguientes opciones es la expresión correcta que debe ir dentro del radical?

1. 5 + (4 × 10) – 6
2. (5 + 4) × (10 – 6)
3. (5 + 4 × 10) – 6
4. 5 + 4 × (10 – 6)

• Para que la expresión  \(3.5 - 1.5 \times 3 \div 6 \times 4 = 4\), sea correcta, el lado izquierdo debe escribirse así:

1. \(\left( {3.5 \,-\ 1.5} \right) \,\times\, 3 \div \left( {6 \,\times\, 4} \right)\)
2. \(3.5\,-\,(1.5 \,×\, 3)\,÷\,6 \,×\, 4\)
3. \(\left[ {\left( {3.5 - 1.5} \right) \,\times\, 3 \div 6} \right] \,\times\, 4\)
4. \(3.5 - \left( {1.5 \,\times\,3 \div 6} \right) \,\times\, 4\)

• ¿A cuál de las siguientes opciones equivale la expresión  \(\frac{(4 \,+\, \frac57)}{9}\)?

1. \(\frac{{\frac{{4 \,+\, 5}}{7}}}{9}\)
2. \(\frac{{4 \,+\, \frac{5}{7}}}{9}\)
3. \(\frac{{4 \,+\, 5}}{{\frac{7}{9}}}\)
4. Todas son equivalentes.

• Una pirámide tiene base cuadrada, su altura mide  h y cada lado de su base mide  x. Si la altura aumenta en 3 unidades de longitud, ¿en cuánto aumenta el volumen de la pirámide?

1. \(3x^2\)
2. \(x^2 h^3\)
3. \(3h\)
4. \(3x^2 h\)

• Si el lado de un cuadrado mide  a y sus cuatro lados aumentan 2 unidades, ¿cuánto aumenta el área del cuadrado?

1. 4a² + 4
2. 4a + 4
3. 4a
4. 4

• El volumen de una pirámide de base cuadrada es  x³. Si el lado de su base mide x, ¿cuánto mide su altura?

1. x
2. x²
3. 3x
4. 3x²

• El área de un rectángulo es  \(9{a^2}b + 3a{b^2}\) y su altura mide \(3ab\). ¿Cuánto mide su base?

1. \(3{\rm{a}} + b\)
2. \(3a + 1\)
3. \(3a\)
4. \(a + 3b\)

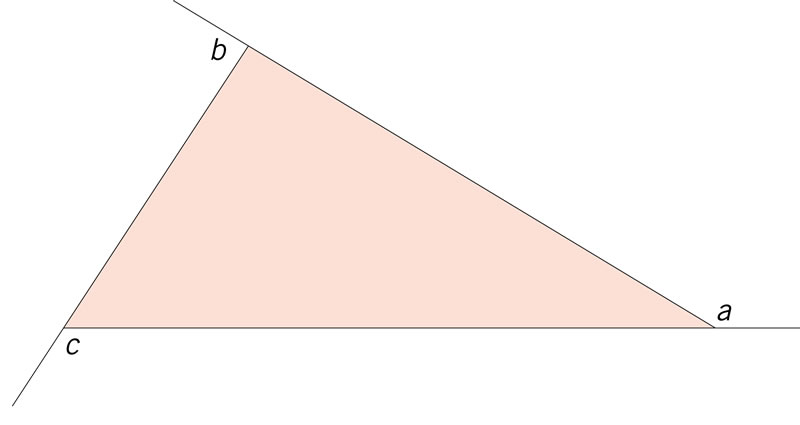
• Considera que el triángulo de la imagen es un triángulo cualquiera. ¿Cuánto suman las medidas de los ángulos a, b y c?


1. 180°
2. 360°
3. 540°
4. 720°

• ¿Cuántos lados tiene el polígono regular cuyos ángulos interiores suman 1 800°?

1. 10
2. 11
3. 12
4. 13

• ¿Cuánto mide cada uno de los ángulos interiores de un octágono regular?

1. 108°
2. 120°
3. 135°
4. 140°

• ¿Con cuál de estos polígonos regulares no puede teselarse el plano?

1. Triángulo equilátero
2. Cuadrado
3. Pentágono
4. Hexágono

• Para hacer una teselación del plano se tiene una cantidad ilimitada de octágonos regulares, como el que se muestra en la imagen, y se requiere otra cantidad también ilimitada de polígonos regulares cuyos lados midan lo mismo que los del octágono. ¿Cuál de las siguientes opciones muestra la forma que se debe elegir para esos otros polígonos?


1. 
2. 
3. 
4. 

• Si una cisterna cúbica tiene capacidad para 8 000 litros de agua, ¿cuál es la longitud de uno de sus lados?

1. 1 m
2. 2 m
3. 4 m
4. 8 m

• ¿Cuál de las siguientes cantidades no equivale a 10 Litros?

  1. 1 daL
  2. 10 000 mL
  3. 10⁻² m³
  4. 1 000 cm³

• Se midió la altura que desciende el nivel del agua en un tinaco al abrir una llave durante ciertos intervalos. Los resultados se muestran en esta tabla.

Tiempo (s)	15	28	30	36
Descenso del nivel de agua(cm)	3	5.6	6	7.2

A partir de los datos se concluyó que la relación entre el descenso del nivel de agua, d, y el tiempo, t, en que permanece abierta la llave se puede expresar como:

1. \(d = \left( {0.2\frac{{{\rm{cm}}}}{{\rm{s}}}} \right)t\)
2. \(d = \left( {5\frac{{{\rm{cm}}}}{{\rm{s}}}} \right)t\)
3. \(d = \left( {0.25\frac{{{\rm{cm}}}}{{\rm{s}}}} \right)t\)
4. \(d = \left( {2\frac{{{\rm{cm}}}}{{\rm{s}}}} \right)t\)

• Considera una pirámide con base cuadrada de lado igual a 3 y altura variable,  h. Se cumple, entonces, una relación de proporcionalidad directa entre la altura y el volumen de la pirámide,  V =  kh donde la constante  k es igual a:

1. \(\frac{1}{3}\)
2. 3
3. 9
4. 27

• Al poner un recipiente (A) bajo una llave abierta, el volumen de agua contenida aumenta según la relación  V = 0.28 t, donde  V es el volumen de agua y  t el tiempo. Otro recipiente (B), colocado bajo la misma llave, se llena de acuerdo con la relación V = 0.31t. ¿Cuál de las siguientes afirmaciones es verdadera?

1. El volumen de los dos recipientes aumenta al mismo ritmo.
2. El volumen en el recipiente A aumenta más rápido que en el recipiente B.
3. El volumen en el recipiente B aumenta más rápido que en el recipiente A.
4. Los dos recipientes tienen la misma capacidad.

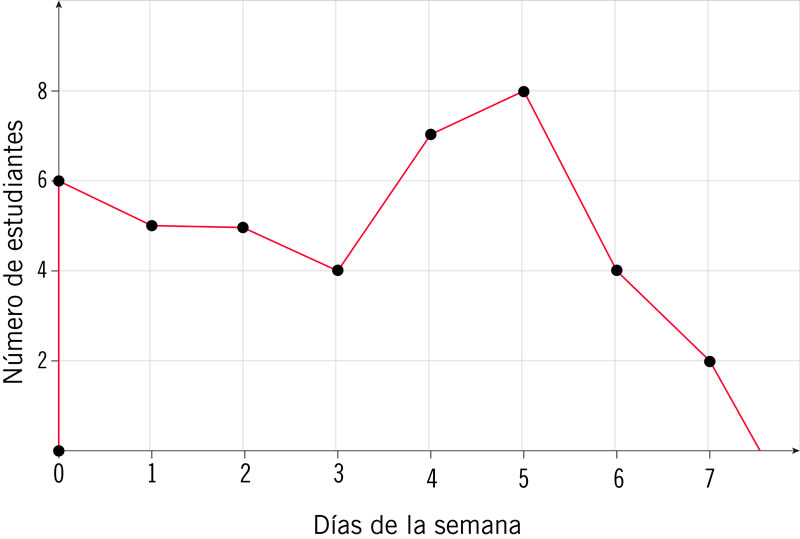
• El histograma de la imagen muestra los resultados de una encuesta realizada a un grupo de jóvenes de secundaria sobre el número de días a la semana que hacen ejercicio. Este último dato se representa en el eje horizontal y en el vertical el número de estudiantes. A partir del histograma, ¿cuál de las siguientes afirmaciones es falsa?


1. Se entrevistó a 41 estudiantes.
2. La mayoría hace ejercicio 5 días a la semana.
3. Hay 20 estudiantes que hacen ejercicio 3 días o menos a la semana.
4. La cantidad de estudiantes que hacen ejercicio 3 o menos días a la semana es la misma la cantidad que hacen ejercicio 4 o más días a la semana.

• Se tienen 5 números distintos y todos menores que 10; si el mayor se triplica, ¿cuál de las siguientes opciones se verifica?

1. La media del conjunto no cambia.
2. La mediana del conjunto no cambia.
3. La mediana del conjunto cambia.
4. La mediana del conjunto se triplica.

• Si se toman 3 números consecutivos de una sucesión con progresión aritmética, ¿cuál de las siguientes opciones se verifica?

1. La media es menor a la mediana.
2. La media es igual a la mediana.
3. La media es mayor a la mediana.
4. La media es el triple de la mediana.

• ¿Cuáles son, respectivamente, los resultados de 4³ + 8 ÷ 4 × 2 y (4³ + (8 ÷ 4)) × 2?

1. 65 y 132
2. 36 y 68
3. 65 y 72
4. 68 y 132

• ¿Cuál es el producto de \((2x + 3)(–x^3 + 1)\)?

1. \(2x^4 + 3x^3 + 2x + 3 \)
2. \(–x^4 – x^3 + 3x + 3 \)
3. \(–2x^4 – 3x^3 + 2x + 3 \)
4. \(–5x^4 + 5x\)

• Expresa el trinomio  \(4x^2\,+\,28x\,+\,49\) como un binomio elevado al cuadrado.

1. \((2x – 7)^2 \)
2. \((2x + 7)^2 \)
3. \((x + 7)^2 \)
4. \((x – 7)^2\)

• ¿Cuál es la suma de los ángulos interiores de un heptágono más la de los ángulos interiores de un pentágono?

1. 236.57°
2. 1 440°
3. 2 160°
4. 1 800°

• Para teselar una cartulina se usaron tres tipos de polígonos regulares, dos de ellos son un triángulo y un cuadrado. En cada vértice de la teselación se unieron dos cuadrados, un triángulo y una pieza del otro polígono regular. ¿Cuál es el tercer tipo de polígono regular?

1. Pentágono
2. Hexágono
3. Heptágono
4. Octágono

• Un recipiente cúbico tiene aristas de 2 dm. ¿Cuántos litros caben en el recipiente?

1. 0.8 L
2. 8 L
3. 80 L
4. 800 L

• Karla compró 3 ramos de flores a $69. ¿Con cuál de las siguientes igualdades se puede representar el precio total de la compra?

1. \(y = kx\)
2. \(69 = 3x + 6 \)
3. \(69 = 5x\)
4. \(y = k + x\)

• Hugo tarda 6 minutos en recorrer una vuelta completa a un parque cuadrado de 110 metros por lado. Si  y representa el tiempo transcurrido y  x, el número de vueltas, ¿qué expresión algebraica indica el tiempo que se demorará Hugo en dar cierta cantidad de vueltas?

1. y = 110x
2. y = 440x
3. 6y = 110x
4. y = 6x

• Con los siguientes datos se hará un histograma: 1, 3, 5, 2 ,4, 6, 5, 11, 3, 3, 2, 1, 0, 0, 6, 13, 4, 3, 1. ¿Cuál es el rango del conjunto de datos?

1. 13
2. 11
3. 10
4. 3.84

• Humberto obtuvo los siguientes puntos en un juego de mesa: 02, 44, 67, 12, 54, 44, 05, 57, 57 y 100. ¿Cuál medida de tendencia central representa mejor el conjunto de datos, la media aritmética o la mediana? ¿Cuánto vale esa medida?

1. La media y su valor es: 44
2. La mediana y su valor es: 49
3. La media y su valor es: 49
4. La mediana y su valor es: 44

Evaluación 3

• ¿Cuál es el décimo término de la sucesión definida por la regla  \(s_n \,=\,4n\,-\,3\)?

1. 33
2. 37
3. 41
4. 43

• El primer término de una sucesión con progresión aritmética es −2 y la diferencia entre sus términos sucesivos es 5. ¿Cuál es el séptimo término de esta sucesión?

1. 18
2. 23
3. 28
4. 33

• El primer término de una sucesión con progresión aritmética es −9 y la diferencia entre sus términos sucesivos es 4. ¿Puede esta sucesión contener el 20; si es así, qué término ocupa?

1. Sí, es el término 8.
2. Sí, es el término 9.
3. Sí, es el término 10.
4. No.

• Tengo tal cantidad de dinero que si la multiplicara por 4 y le sumara 10 daría lo mismo que si primero le sumara 10 y el resultado lo multiplicara por 3. ¿Cuánto dinero tengo?

1. 15
2. 20
3. 25
4. 30

• Julio tenía cierta cantidad de canicas y Verónica el doble. Ella le dio a Julio 7 de sus canicas y ahora ambos tienen la misma cantidad. ¿Cuántas canicas tenía Julio?

1. 21
2. 10
3. 14
4. 7

• Si la masa de una roca es \(\frac12\) kg más la mitad de su propia masa, ¿cuál es su masa?

1. \(\frac12\) kg
2. 1 kg
3. \(\frac32\) kg
4. 2 kg

• La suma de 3 números consecutivos es igual al triple de la mitad del primero. ¿Cuál es el mayor de estos números?

1. −2
2. 0
3. 1
4. 2

• En una circunferencia se toman puntos  A y  C, que son diametralmente opuestos; se traza la mediatriz del segmento  \(\overline {AC} \) y se nombran las intersecciones entre ésta y la circunferencia como  B y  D, respectivamente. La figura  ABCD es un:

1. Trapecio
2. Rectángulo
3. Cuadrado
4. Rombo

• En la imagen, el segmento  \(\overline {AB} \) es un diámetro de la circunferencia y el punto  C se encuentra sobre la circunferencia; entonces:


1. \(\overline {AC} + \overline {BC} = \overline {AB} \)
2. El segmento \(\overline {AC} \) es una altura del triángulo \(ABC\).
3. El segmento \(\overline {AC} \) forma un ángulo de 45° con el segmento  \(\overline {AC} \).
4. Mide la mitad del segmento  \(\overline {AB} \).

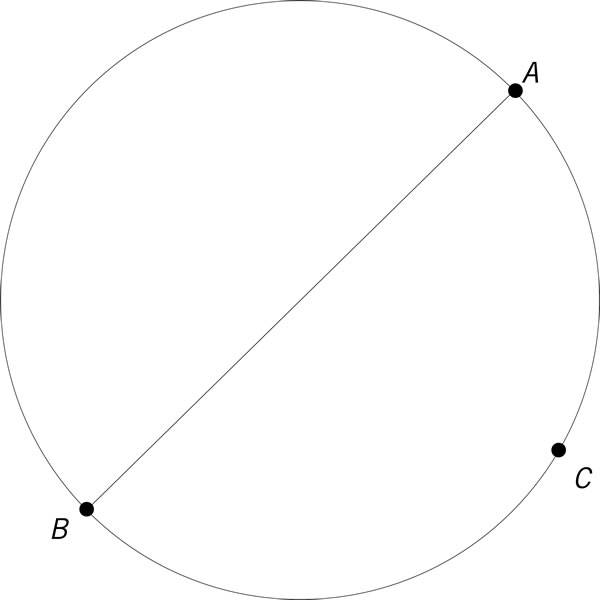
• Si un cuadrilátero tiene todos sus vértices sobre una circunferencia, sus ángulos opuestos suman:

1. 360°
2. 180°
3. 90°
4. 60°

• Si se unen los puntos de la gráfica de una relación de proporcionalidad directa y la figura formada se extiende, se tendrá una línea recta que:

1. Es paralela al eje X.
2. Pasa por arriba del origen.
3. Pasa por el origen.
4. Pasa por debajo del origen.

• ¿Cuál de los siguientes puntos sí podría pertenecer a la gráfica de alguna relación de proporcionalidad inversa?

1. (5, 0.2)
2. (1, 0)
3. (0, 1)
4. (0, 0)

• Dos cantidades, h y t, varían en todos los números reales de acuerdo con la relación
  h = at + b, donde a y b con constantes. Para que esta relación sea de proporcionalidad directa, ¿cuál de los términos debería ser igual a 0?

1. h
2. a
3. t
4. b

• La tarifa de un taxi está dada por el banderazo inicial de $9.00 más $4.00 por cada kilómetro recorrido. ¿Cuál de las siguientes opciones indica el costo por viaje en términos de la distancia recorrida? Considera que  p es el costo y  d la distancia recorrida.

1. \(p = 9d + 4\)
2. \(p = 4d + 9\)
3. \(p = 9d - 4\)
4. \(p = 4d\)

• Para convertir una temperatura de grados Celsius (c) a Kelvin (k) sólo hay que restar 273 a la temperatura en grados Celsius. ¿Cuál de las siguientes afirmaciones es verdadera?

1. k varía de modo directamente proporcional a  c.
2. k varía de modo inversamente proporcional a  c.
3. k varía cuadráticamente respecto a  c.
4. k varía linealmente respecto a  c.

• ¿Cuál de las siguientes expresiones no corresponde con una variación lineal?

1. \(y = ax + b \)
2. \(yx = k\)
3. \(y = mx\)
4. \(k = \frac{y}{x}\)

• La empleada de una tienda de ropa tiene un sueldo base de $2 400.00 más una comisión de $60.00 por cada prenda vendida. ¿Cuántas prendas debe vender, como mínimo, para que esta quincena cobre más de $4 000.00?

1. 25
2. 26
3. 27
4. 28

• En cierta ciudad, un viaje de 5 km en taxi cuesta $35.00 y uno de 8 km, $50.00. Traza la gráfica en el siguiente plano y considerando que la relación entre la distancia y el costo del viaje es lineal, se concluye que en esta ciudad el banderazo es de:


1. $14.00
2. $10.00
3. $8.00
4. $5.00

• El examen final de un curso se valora como tres veces un examen parcial. Si un estudiante tiene una calificación en el examen final de 6 y parciales de 7 y 9, ¿cuál es su calificación definitiva?

1. 7.3
2. 6.8
3. 7.2
4. 8

• Un profesor evalúa su curso con dos exámenes ordinarios y uno final, que vale más que un ordinario. Un estudiante que con los ordinarios obtuvo 7 y 7 y en el final 8, sacó una calificación total de 7.5. ¿Cuántas veces más que un ordinario vale el examen final?

1. 4
2. 3
3. 2
4. 1.5

• ¿Cuáles son los primeros cinco números de la sucesión: 8x − 5?

1. 0, –3, –11, –19, –27
2. –3, –11, –19, –27, –35
3. 3, 11, 19, 27, 35
4. 0, 3, 11, 19, 27

• ¿Cuál es el término que ocupa la posición 8 en la sucesión:
  4x − 2.5?

1. 29.5
2. –29.5
3. 22
4. –22

• ¿Cuál es el valor de x en la siguiente ecuación:
  \(\frac36\) (3x − 2) = x − 12?

1. 11
2. 0.5
3. 5.5
4. –22

• ¿En cuál ecuación  \(x = 7\) satisface la igualdad?

1. \(\frac{4}{x\,-\,3} = \frac{5}{x\,-\,2}\)
2. \(4x\,-\,12 = 5x \,-\, 10\)
3. \(\frac{4}{x\,+\,2} = \frac{5}{x\,+\,2}\)
4. \(\frac{5}{x\,-\,3} = \frac{2}{x\,-\,2}\)

• En una semicircunferencia, ¿cuánto mide el ángulo que sólo toca los puntos extremos del diametro y cualquier otro punto sobre la semicircunferencia?

1. 22.5°
2. 180°
3. 90°
4. 45°

• ¿Cuál es la ecuación que la describe la siguiente gráfica?


1. \(y = 2x\)
2. \(y = x \)
3. \(y = \frac{x}{2}\)
4. \(y = -\frac{x}{2}\)

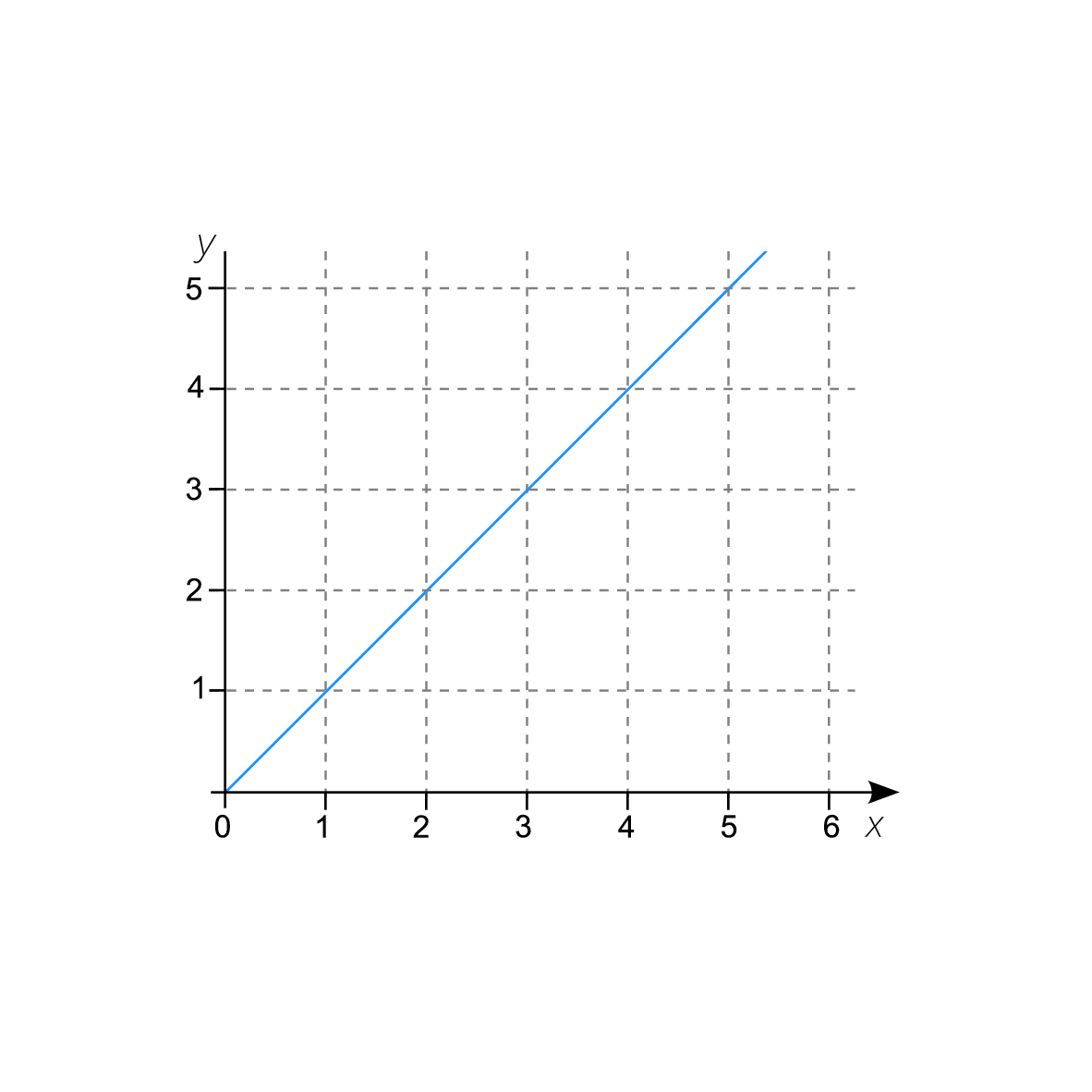
• ¿Qué gráfica corresponde a la ecuación: y = \(\frac{3}{2} x\)


1. Imagen 1
2. Imagen 2
3. Imagen 3
4. Imagen 4

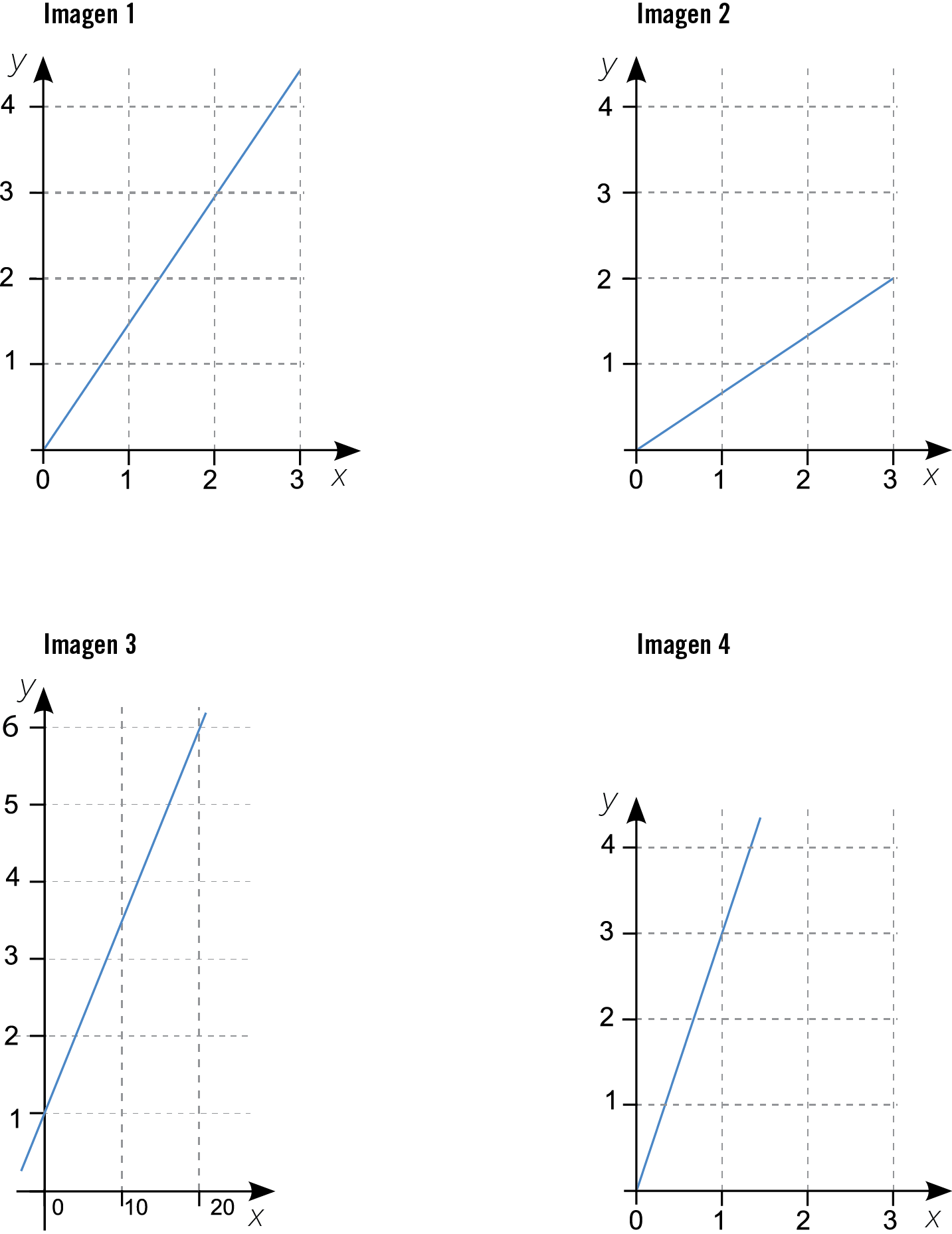
• José trabaja vendiendo galletas. Su sueldo semanal es de $850 y por cada caja de galletas que venda gana $13. Si la semana pasada José recibió un sueldo total de $1 019, ¿cuántas cajas de galletas vendió?

1. 2 cajas
2. 65 cajas
3. 78 cajas
4. 13 cajas

• Sergio jugó un videojuego en el cual debía recolectar estrellas. Comenzó con 5 y cada día conseguía 24 estrellas más. ¿Qué expresión algebraica describe el número de estrellas que recolectó?

1. 24xn + 5, donde n es el número de días que juega Sergio.
2. \(5xn + 24 \), donde n es el número de días que juega Sergio.
3. \((5 + 24)\,xn\), donde n es el número de días que juega Sergio.
4. 24n, donde n es el número de días que juega Sergio.

• Daniel ayudó a empacar chocolates en cajitas sorpresa. Sobre cada una anotó el número de chocolates que colocó en ellas: en 3 cajas anotó 32 chocolates, en 5 cajas anotó 20, en 9 cajas anotó 12 y en 2 cajas anotó 35 chocolates. ¿Cuál es el promedio de chocolates que Daniel empacó en las cajas?

1. Aproximadamente 4 chocolates
2. Aproximadamente 20 chocolates
3. Aproximadamente 5 chocolates
4. Aproximadamente 18 chocolates

• Si la suma de cualquier par de ángulos internos de un triángulo es 120°, entonces el triángulo es...

1. Isósceles
2. Equilátero
3. Escaleno
4. Obtusángulo

• En una quermés escolar, Enrique vendió tacos y tostadas a $4.00 y $7.00 la pieza, respectivamente; en total vendió 30 piezas con lo que reunió $156.00. El número de tacos vendidos excedió al de tostadas vendidas en:

1. 4
2. 5
3. 6
4. 7

• Durante el año, Andrea ahorró solamente monedas de 2 y 5 pesos; en navidad rompió su alcancía y descubrió que había acumulado 73 monedas, y en total había ahorrado 218 pesos. ¿Cuántas monedas de 2 pesos había en la alcancía?

1. 24
2. 31
3. 43
4. 49

• Si al graficar un sistema de ecuaciones de 2 × 2 se obtienen dos rectas perpendiculares entre sí, el sistema tiene:

1. Ninguna solución.
2. Una solución.
3. Dos soluciones.
4. Muchas soluciones.

• La gráfica muestra dos rectas que corresponden al sistema de ecuaciones:


1. \(\left\{ {\begin{array}{*{20}{c}}{x + 2y = 8}\\{x - y = 1}\end{array}} \right.\)
2. \(\left\{ {\begin{array}{*{20}{c}}{x - 2y = 8}\\{x + y = 1}\end{array}} \right.\)
3. \(\left\{ {\begin{array}{*{20}{c}}{2x - 2y = 8}\\{x + y = 1}\end{array}} \right.\)
4. \(\left\{ {\begin{array}{*{20}{c}}{2x + y = 8}\\{x - y = 1}\end{array}} \right.\)

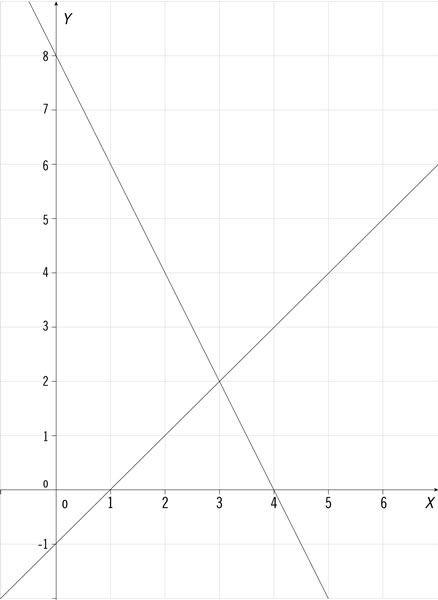
• ¿Cuál de los siguientes sistemas tienen como gráficas un par de rectas paralelas entre sí?

1. \(\left\{ {\begin{array}{*{20}{c}}{x - 3y = 1}\\{ - 4x + 12y = - 4}\end{array}} \right.\)
2. \(\left\{ {\begin{array}{*{20}{c}}{2x + y = 8}\\{x - y = 1}\end{array}} \right.\)
3. \(\left\{ {\begin{array}{*{20}{c}}{x + y = 3}\\{x - y = 1}\end{array}} \right.\)
4. \(\left\{ {\begin{array}{*{20}{c}}{x - y = 1}\\{x + y = 2}\end{array}} \right.\)

• ¿Cuál de las siguientes figuras tiene más ejes de simetría?

1. Cuadrado
2. Rectángulo
3. Triángulo equilátero
4. Triángulo isósceles

• Los polígonos irregulares A y B son simétricos entre sí respecto a un eje, ¿qué elemento los distingue?

1. Sus ángulos
2. Sus longitudes
3. Su orientación
4. El número de sus lados

• Se recorta en cartón una figura geométrica cuya característica es que si se fija de su centro sobre una hoja cuadriculada, siempre que se gire 60° tendrá la misma disposición respecto al rayado del papel; entonces la figura es un...

1. Triángulo equilátero.
2. Cuadrado.
3. Pentágono.
4. Hexágono.

• ¿Cuál de las figuras, al girarla 120° sobre su centro, coincide con su posición original?

1. Triángulo escaleno
2. Triángulo equilátero
3. Cuadrado
4. Pentágono

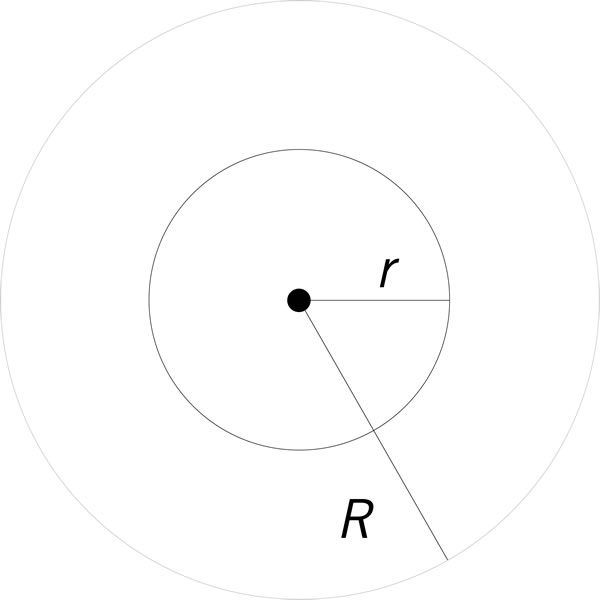
• Si el área de la corona circular que se muestra en la imagen es el cuádruple del área del círculo interior, ¿cuál es la medida del radio del círculo exterior  (R)?


1. 2r
2. 3r
3. 4r
4. 5r

• De un aro delgado de hierro, cuyo radio es de 1 m, se desea cortar un arco para enderezarlo y obtener una varilla de 1 m de largo. ¿Qué ángulo corresponde al arco cortado?

1. 57.3°
2. 48.1°
3. 45°
4. 30.6°

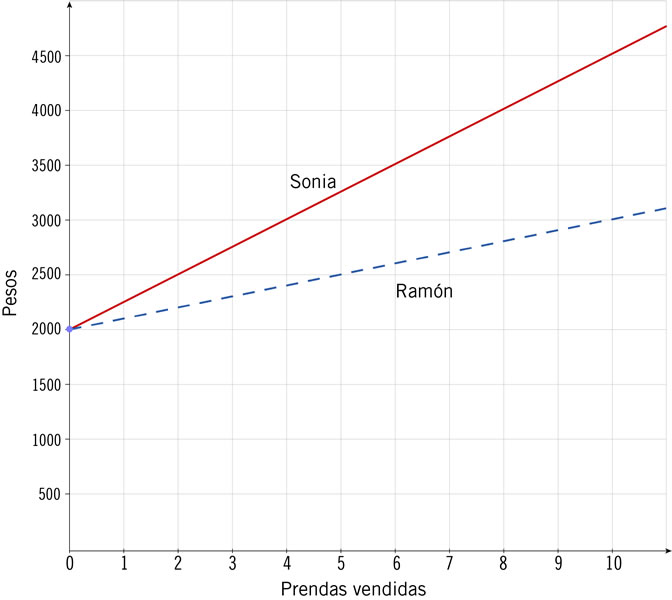
• Sonia y Ramón trabajan en una tienda de ropa y ambos tienen sueldos base y comisiones fijas por cada producto que venden. La gráfica muestra las relaciones entre sus sueldos y el número de prendas que venden. Con base en ellas, ¿cuál de las siguientes afirmaciones es verdadera?


1. Sonia tiene sueldo base menor que el de Ramón.
2. Sonia tiene sueldo base mayor que el de Ramón.
3. La comisión de Sonia es menor que la de Ramón.
4. La comisión de Sonia es mayor que la de Ramón.

• Para convertir una temperatura de grados Celsius a grados Fahrenheit se usa la expresión\({T_F} = \frac{9}{5}{T_C} + 32\). Si graficamos esta relación en un plano cartesiano con los valores de temperatura en grados centígrados  (T_C) en el eje horizontal y los de grados Fahrenheit  (T_F) en el vertical, ocurre que:

1. La gráfica pasa por el origen.
2. La gráfica corta al eje horizontal en 32.
3. La gráfica corta al eje vertical en 32.
4. La gráfica corta al eje vertical en –32.

• Un objeto se mueve en línea recta, de modo que su posición queda descrita por la expresión \(y = mt + b\), donde t es el tiempo. Si el objeto duplica su velocidad, ¿qué expresión describirá entonces su movimiento?

1. \(2y = mt + b\)
2. \(y = mt + 2b\)
3. \(y = 2mt + b\)
4. \(y = {m^2}t + b\)

• ¿Cuál es el punto de intersección de las rectas dadas por las expresiones  \(y = 2mx + b\) y \(y = 3mx + b\)?

1. (2, 3)
2. (2m, 3m)
3. (0, b)
4. (b, 0)

• Se propone una ecuación  \(y = mx + b\) cuya gráfica sea una recta paralela a la gráfica de la ecuación \(y = 7.3x - 11.4\), entonces es necesario elegir:

1. \(m = - 7.3,b = 11.4\)
2. \(m = - 7.3,b \ne {\rm{ }}11.4\)
3. \(m = 7.3,b = - 11.4\)
4. \(m = 7.3,b \ne - 11.4\)

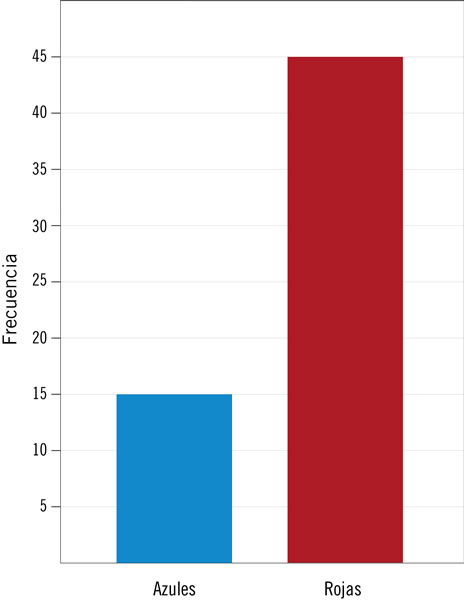
• En una bolsa oscura hay 10 canicas de color rojo y azul, todas del mismo tamaño. Carmen realizó el siguiente experimento 60 veces: extrajo una canica al azar, registró su color y la devolvió a la bolsa. Con base en la gráfica que muestra los resultados, ¿cuál de las siguientes afirmaciones es más razonable?


1. Hay igual número de canicas rojas que de azules.
2. Hay más canicas rojas que azules.
3. El número de canicas rojas es el doble que el de las azules.
4. Hay menos canicas rojas que azules.

• Dos dados se lanzan 1 000 veces, y al construir la gráfica de la distribución de frecuencias de los resultados se esperaría que el número de veces que la suma de los dados dio 7, fuera cercano a:

1. 7
2. 333
3. 167
4. 500

• Se lanza un volado 100 veces, y se esperaría que el número de veces que sale águila sea:

1. 10
2. 25
3. 50
4. 75

• ¿Cuál es la solución del siguiente sistema de ecuaciones:
  \(5x\,+\,2y\,=\,8\) y \(4x\,−\,5y\,=\,2\)?

1. \(x = \frac23\) , \(y = \frac43 \)
2. \(x = \frac43\) , \(y = \frac23 \)
3. \(x = \frac34\) , \(y = \frac32 \)
4. \(x = \frac32\) , \(y = \frac34 \)

• ¿De qué sistema  \(y =\frac13\), \(x=\frac13\) son solución?

1. \(2x + 16y = 6\)  y  \(4x + 8y = 4 \)
2. \(16x + 2y = 6\)  y  \(8x + 2y = 4 \)
3. \(4x + 16y = 8\)  y  \(3x + 8y = 3 \)
4. \(5x + 2y = 5\)  y  \(4x − 3y = 1\)

• Observa la gráfica y a partir de ella selecciona el enunciado correcto.


1. x = 2, y = 0 es la solución del sistema de ecuaciones
2. La ecuación de la recta punteada es  \(2x + y = 4\)
3. La ecuación de la recta continua es  \(2x + 3y = 4\)
4. El sistema de ecuaciones tiene muchas soluciones

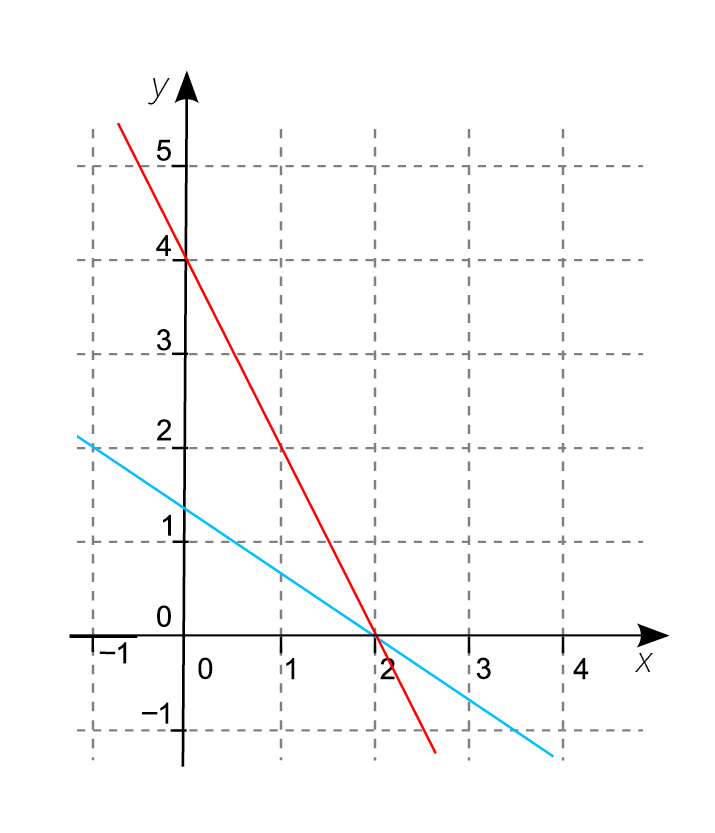
• En la gráfica el punto A es la solución de un sistema de ecuaciones, de las cuales sólo se ha representado una. ¿Cuál de las siguientes expresiones corresponde a la otra ecuación?


1. 2x + 2y = 4
2. 2x + 2y = 5
3. x + y = 1
4. x − y = 2

• ¿Cuál de los siguientes enunciados es verdadero para dos figuras simétricas?

1. La longitud de sus lados y sus ángulos son diferentes en ambas figuras.
2. Sólo la longitud de sus lados son las mismas en las dos figuras.
3. Sólo los ángulos son los mismos en las dos figuras.
4. Los ángulos y la longitud de sus lados son los mismos en las dos figuras.

• ¿Cuál es el área de un sector circular que tiene un ángulo central de 60° y forma parte de una circunferencia de 4 cm de radio?

1. 40.8 cm²
2. 12.57 cm²
3. 8.37 cm²
4. 2.10 cm²

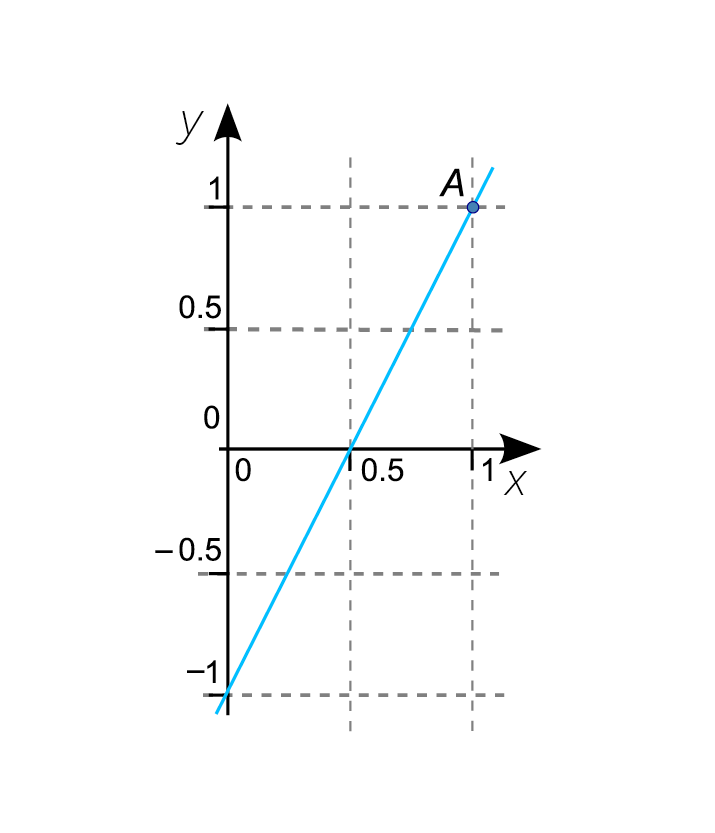
• ¿Cuál es el la ecuación que corresponde a la gráfica?


1. \(y = 10x + 5 \)
2. \(x = 5y + 10 \)
3. \(y = 5x + 10\)
4. \(x = 10y + 5\)

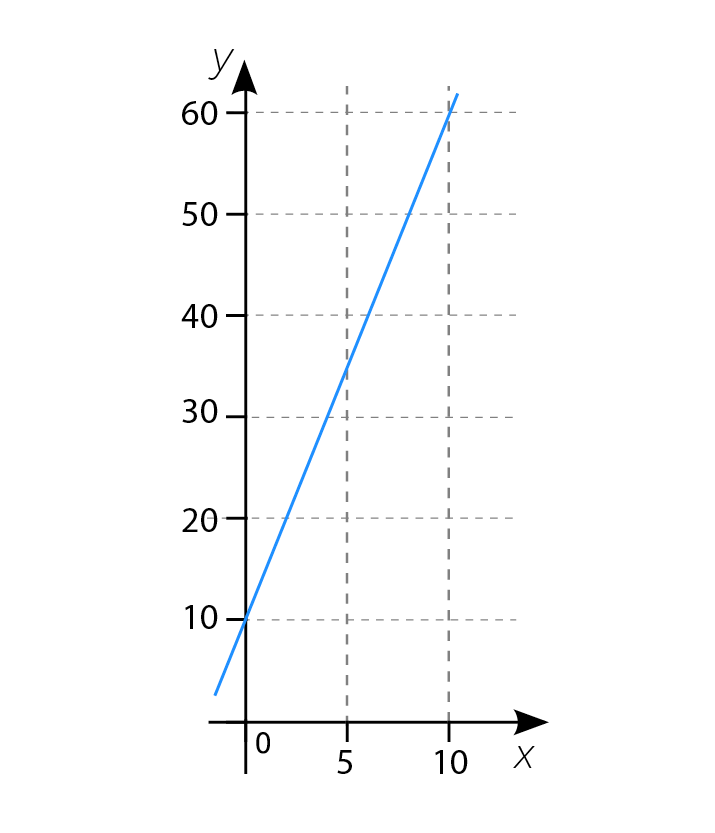
• ¿Cuál es la ecuación que corresponde a una gráfica paralela a la de la figura?


1. \(3x + y = 12 \)
2. \(2x + 6y = 12 \)
3. \(6x + 2y = 1 \)
4. \(x + y = 1\)

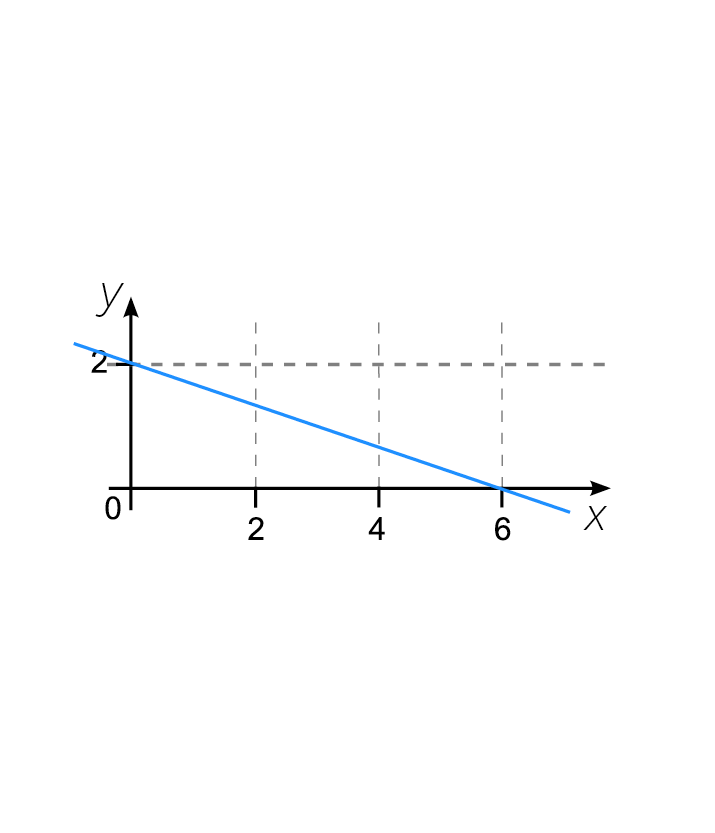
• ¿Cuál de los siguientes enunciados es correcto para las ecuaciones  \(y = ax + b\) y  \(y = cx + b\,con\,c ≠ a\)?

1. Las gráficas son paralelas.
2. Las gráficas tienen diferente pendiente.
3. Las gráficas son iguales.
4. Las gráficas son inversas.

• ¿Qué se tiene que hacer para que la gráfica de distribución teórica de un experimento se parezca mucho a su gráfica de distribución frecuencial?

1. Las gráficas en todos los experimentos ya se parecen.
2. Realizar el experimento una vez.
3. Realizar el experimento una cantidad considerable de veces.
4. Las gráficas no se pueden parecer.

Examen final