Las ecuaciones cuadráticas deben su nombre...
El cuadrado de la edad de Sandra hace nueve años es igual a la edad que tendrá dentro de nueve años. Si la edad actual de Sandra se representa con la letra s, ¿cuál de las siguientes ecuaciones cuadráticas representa esta situación?
El piso de un salón es un rectángulo cuyo largo mide el doble que su ancho y su área coincide numéricamente con su perímetro. ¿Qué ecuación cuadrática representa esta situación?
¿Cuál de las siguientes parejas de números al elevarlos al cuadrado y restarles 9 son iguales a 7?
Los triángulos que se forman al dividir un paralelogramo con una diagonal son:
Las diagonales de un paralelogramo se cortan en sus puntos medios. ¿Qué argumento justifica esta afirmación? Considera la siguiente figura.
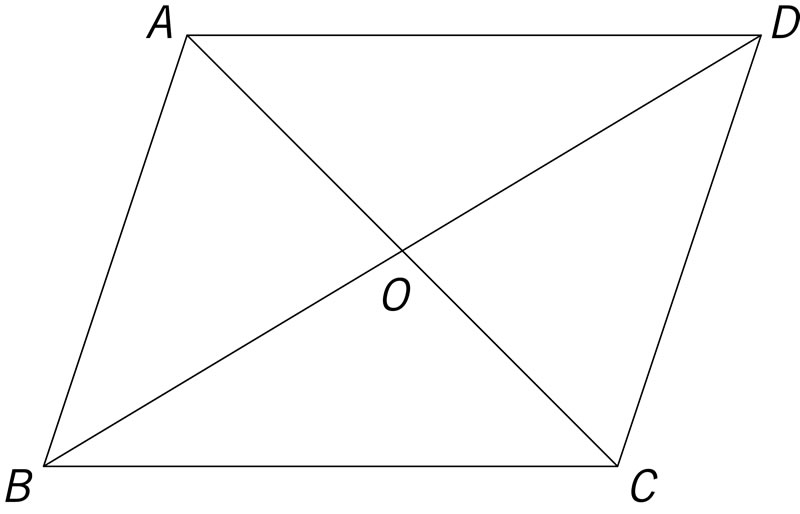
¿Cuál de las siguientes afirmaciones es falsa?
¿Qué parámetros deben cumplirse para asegurar que dos triángulos o dos cuadriláteros son semejantes?
¿En cuál de los siguientes casos no se obtienen, necesariamente, triángulos congruentes?
¿Cuál de las siguientes afirmaciones es incorrecta respecto a la semejanza entre dos triángulos?
¿Qué gráfica corresponde a los valores de la tabla?
| x | 3 | 6 | 9 | 12 | 15 |
| y | 2.5 | 4 | 5.5 | 7 | 8.5 |
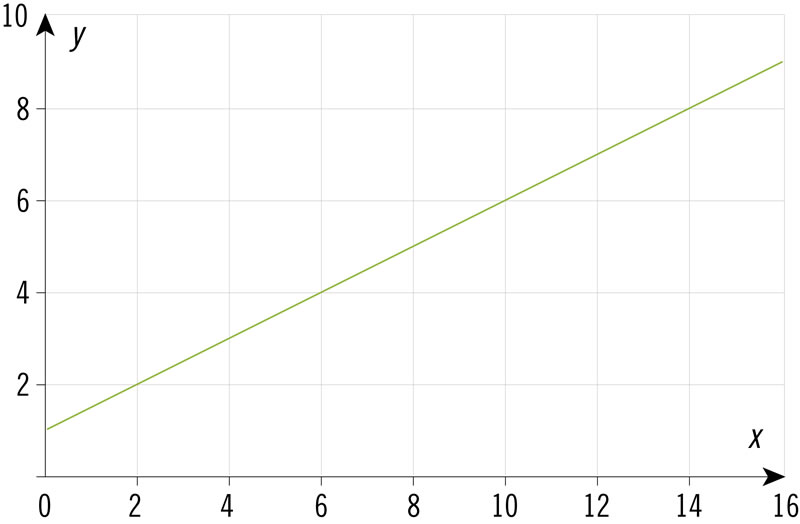
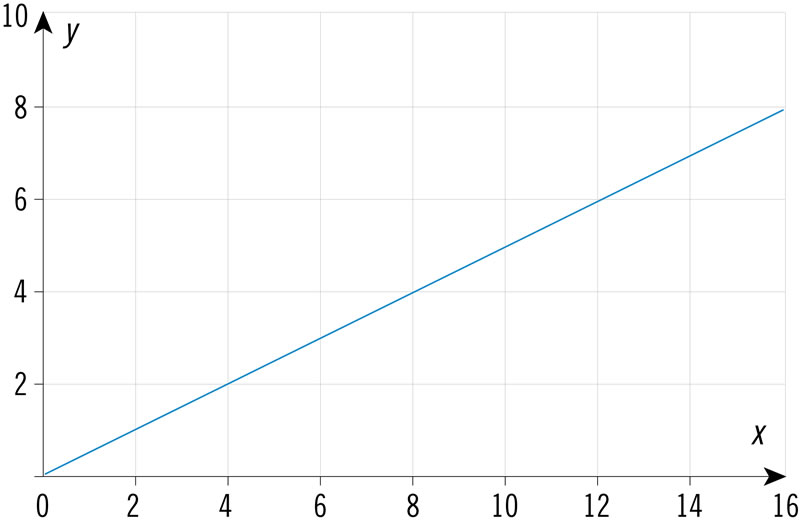
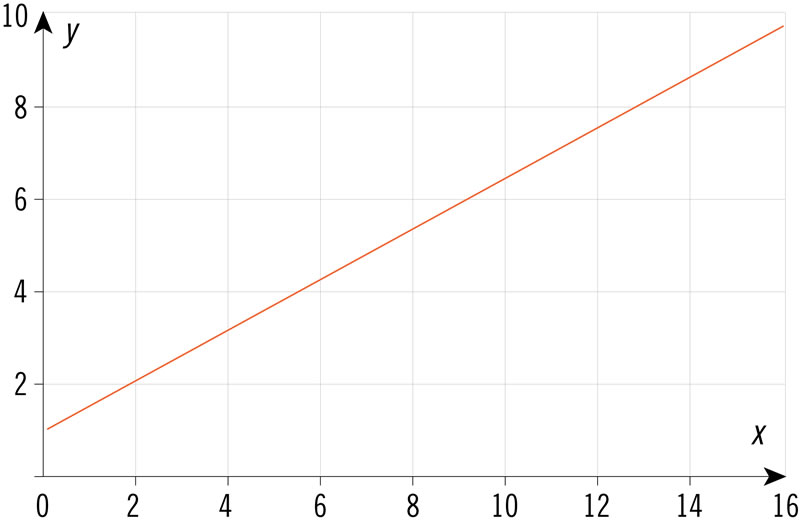
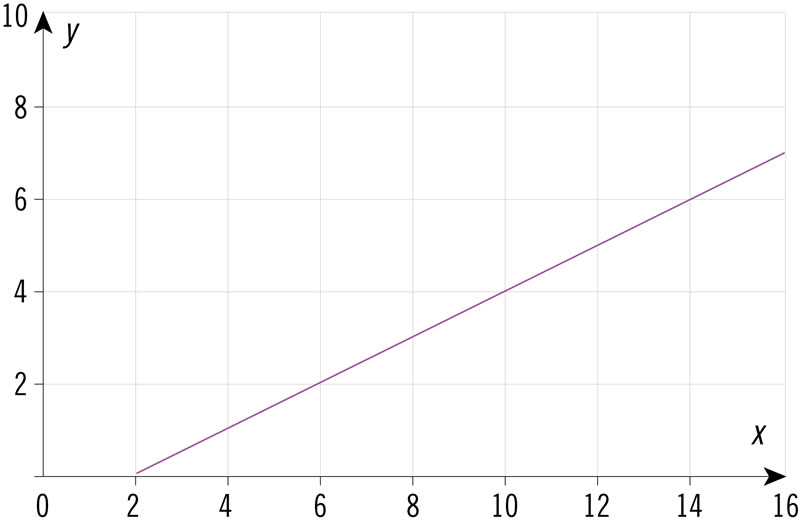
¿Qué expresión algebraica corresponde a los valores de la tabla?
| x | 3 | 6 | 9 | 12 | 15 |
| y | 2.5 | 4 | 5.5 | 7 | 8.5 |
¿Cuál de las gráficas representa una relación de proporcionalidad directa?
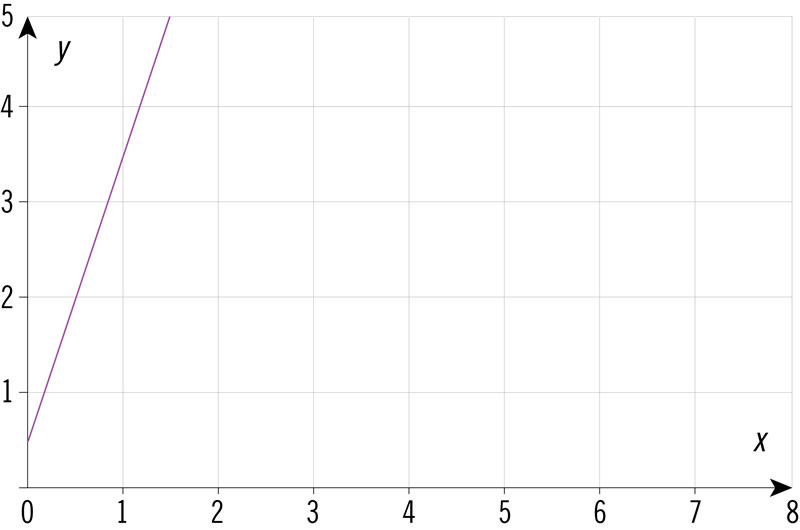
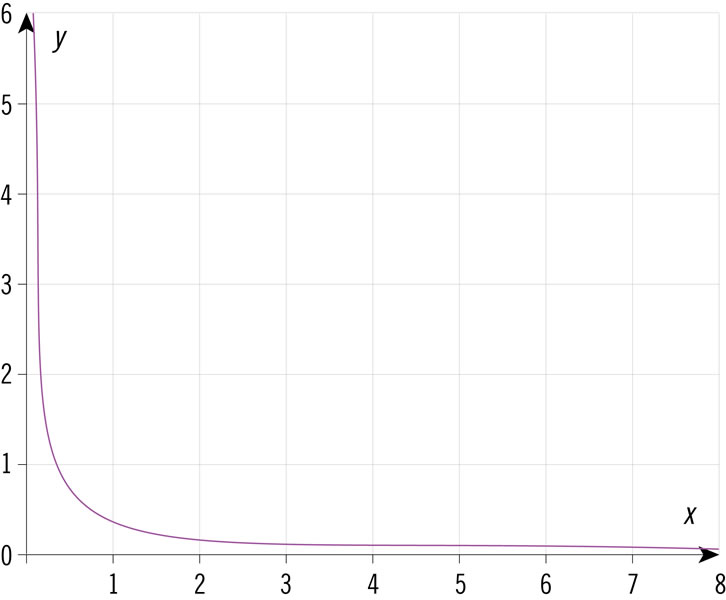
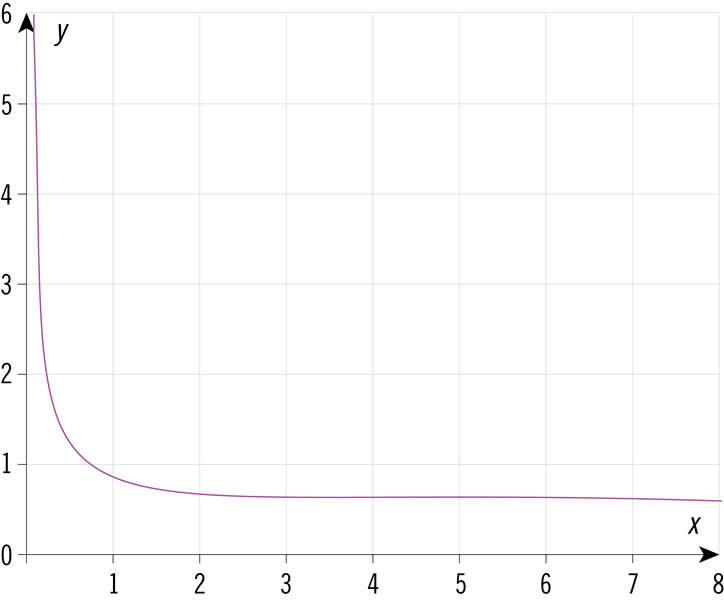
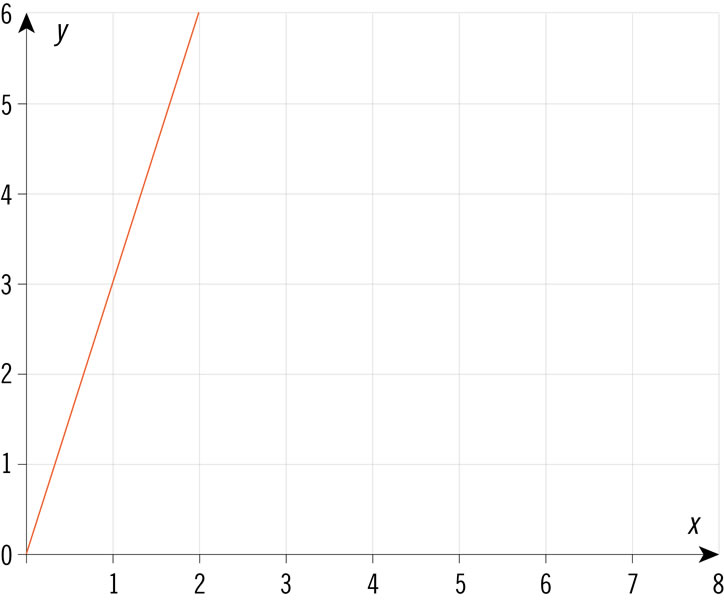
Las ganancias de una empresa se definen por la ecuación G = 0.08c2 − 0.1c + 2, donde G son las ganancias y c el capital invertido, ambos en miles de pesos. ¿Qué tabla representa esa situación?
| c | 10 | 20 | 30 | 40 | 50 |
| G | 9 | 32 | 71 | 126 | 197 |
| c | 10 | 20 | 30 | 40 | 50 |
| G | 7 | 32 | 69 | 126 | 195 |
| c | 10 | 20 | 30 | 40 | 50 |
| G | 9 | 32 | 71 | 124 | 197 |
| c | 10 | 20 | 30 | 40 | 50 |
| G | 7 | 32 | 69 | 124 | 195 |
La siguiente tabla muestra las ganancias g (en pesos) obtenidas por fabricar y vender n unidades de audífonos.
| n | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| g | 700 | 1 200 | 1 500 | 1 600 | 1 500 | 1 200 | 700 |
A partir de la tabla, ¿qué tipo de relación existe entre las ganancias y el número de audífonos?
La tabla que se muestra a continuación presenta valores que se pueden expresar con la ecuación:
| x | 1 | 2 | 3 | 4 | 5 |
| y | −10 | 10 | 50 | 110 | 190 |
La temperatura a la que hierve el agua depende de la altitud sobre el nivel del mar a la que se encuentre, según la fórmula: \(h = 1000\left( {100{\rm{ }}-T} \right) + 580{(100-T)^2}\), donde T es la temperatura en grados Celsius, y h la altitud en metros. La ecuación es válida para el rango \(95^\circ C \le T \le 100^\circ C\). ¿A qué temperatura hierve el agua en la cima del monte Éverest, cuya altura es de 8 840 m? Señala la ecuación que modela esta situación. Para simplificar cálculos sustituye \({(100 - T)^2} = {x^2}\).
La ecuación para calcular, en cualquier instante, la altura de un objeto que se lanza verticalmente hacia arriba es \(h = - 4.9{t^2} + {v_0}t\), donde \({v_0}\) es la velocidad inicial y h, la altura. Si el objeto se lanza con una velocidad inicial de 400 m/s, ¿qué ecuación permite calcular el tiempo que tardará en regresar al punto de lanzamiento?
Si P(x) es la probabilidad de ocurrencia de un evento x, ¿qué par de desigualdades es correcta?
Un experimento aleatorio consiste en lanzar dos monedas al aire y, al caer, considerar la cara superior de cada una. Si el resultado es {S, A} donde S representa sol y A, águila, ¿cuál de los siguientes eventos es su evento complementario?
Dos eventos son independientes si...
Si se quiere conocer la preferencia electoral de los ciudadanos de un país por un candidato a presidente nacional, es conveniente...
Para realizar una encuesta y representar los resultados, los pasos a seguir son...
El objetivo de una encuesta es conocer la opinión de los adolescentes de 12 a 16 años de todo el país sobre las redes sociales. ¿Cuál de los siguientes grupos de personas es una muestra representativa de la población de estudio?
La altura de un triángulo mide el triple de su base y su área es de 45
¿Cuál o cuáles son los posibles valores de x en la igualdad \(x^{2}-13=-4\) ?
Dos triángulos son semejantes entre sí. Los ángulos de uno miden, respectivamente, 90°, 40° y 50°. ¿Cuáles son las medidas de los ángulos del otro?
La constante de proporcionalidad entre los lados de dos rectángulos semejantes es 1.6. ¿Cuáles son las medidas de uno de los rectángulos, si el otro tiene 8 cm de base y 3.5 cm de altura?
Los lados de un triángulo miden 8 cm, 3 cm y 4 cm y los lados de otro triángulo miden 12 cm, 4.5 cm y 6 cm. ¿Cómo son entre sí los ángulos de los dos triángulos y cómo justificas tu respuesta?
En una feria de libros a los estudiantes se les otorga 45% de descuento en la compra de cualquier libro. Si un estudiante compra un libro con un costo de x pesos, ¿con qué expresión se puede calcular lo que pagará?
La distancia que ha recorrido una motocicleta durante cierto número de horas se representa con la expresión d = 85t. Si al trazar la gráfica que representa la expresión anterior en el eje vertical se coloca el tiempo transcurrido, ¿qué punto del plano cartesiano corresponde a un tiempo de 2.5 horas?
¿Cuál de las siguientes expresiones algebraicas corresponde con los valores de la tabla?
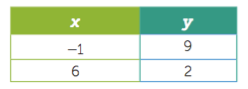
¿Cuál es la probabilidad de seleccionar un número par si el espacio muestral es {0, 2, 4, 6, 8, 10, 12, 14}?
¿Cuál sería una muestra representativa de una encuesta si se quiere conocer las preferencias musicales de los adolescentes?
La ecuación x2 − 2x − 3 = 0 se puede expresar como:
La ecuación m2 = 9 se puede expresar como:
Si el producto de (a + 3) por (a − 15) es igual a cero, entonces:
El producto de un número más cinco unidades, multiplicado por el mismo número menos dos unidades es igual a cero. ¿Cuál o cuáles números cumplen esta condición?
El largo de un rectángulo es dos unidades más grande que su ancho y su área es de tres unidades cuadradas. ¿Cuánto mide el ancho del rectángulo?
¿Cuál de las siguientes afirmaciones es correcta?
¿Cuál de las afirmaciones es incorrecta?
Un pentágono irregular se rotó 90° en sentido horario con respecto a un punto de rotación O. La figura resultante se rotó otra vez, con centro de rotación O, 450° en sentido antihorario. ¿Cuál es la relación entre el primero y el último pentágono?
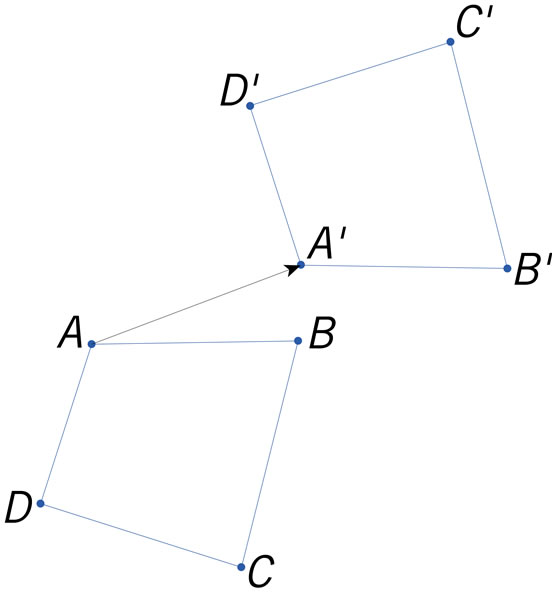
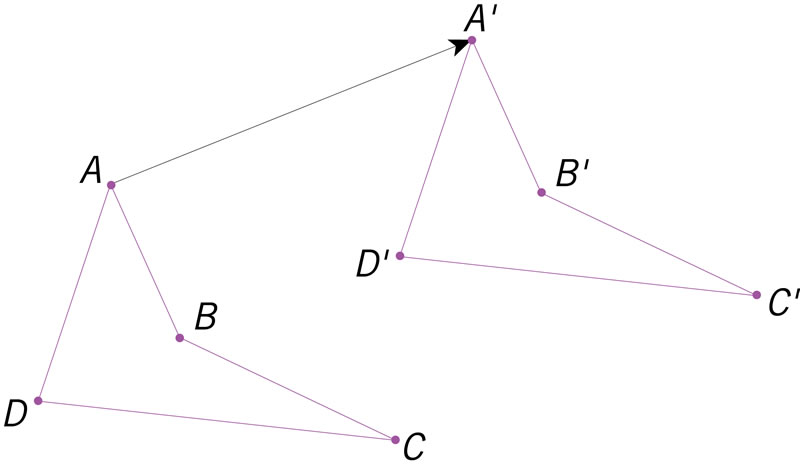
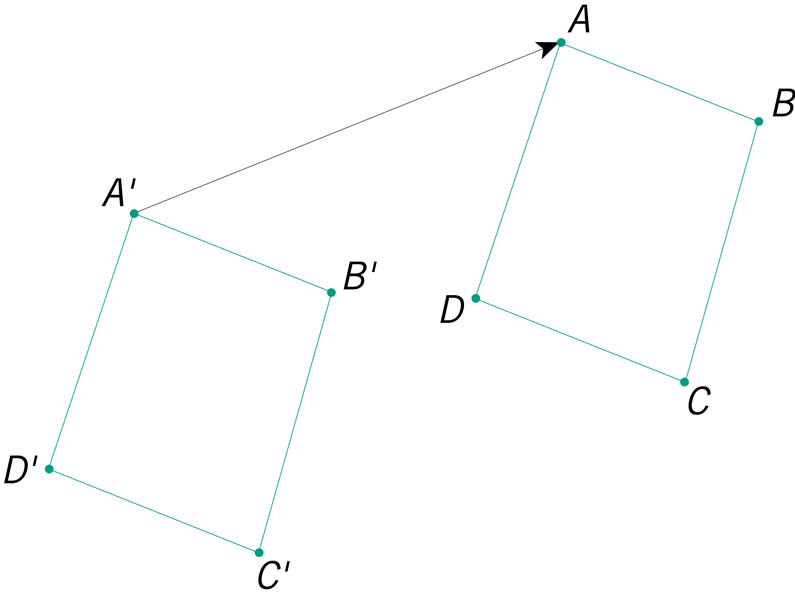
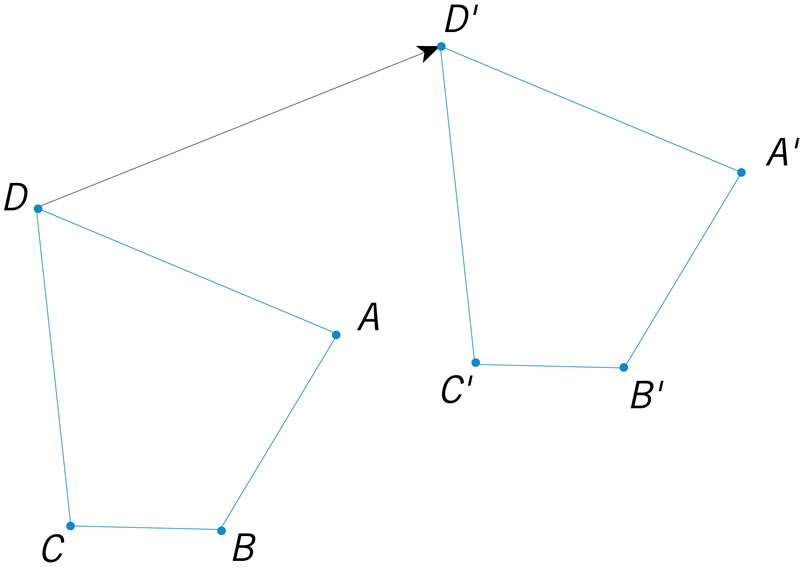
¿Qué figura representa una traslación del cuadrilátero ABCD con directriz \(\overrightarrow {AA'}\)?
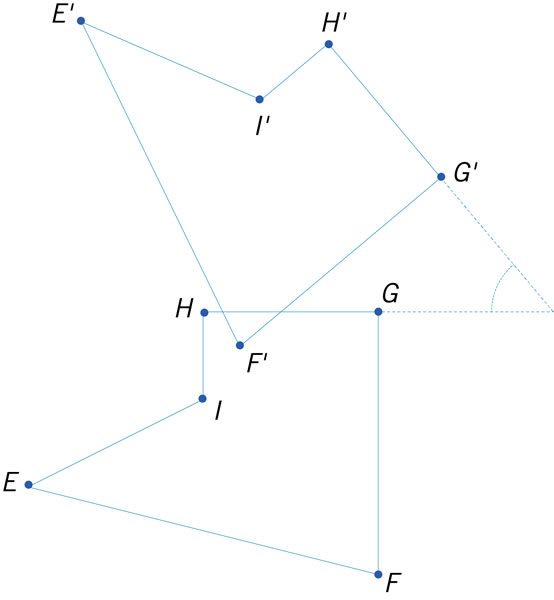
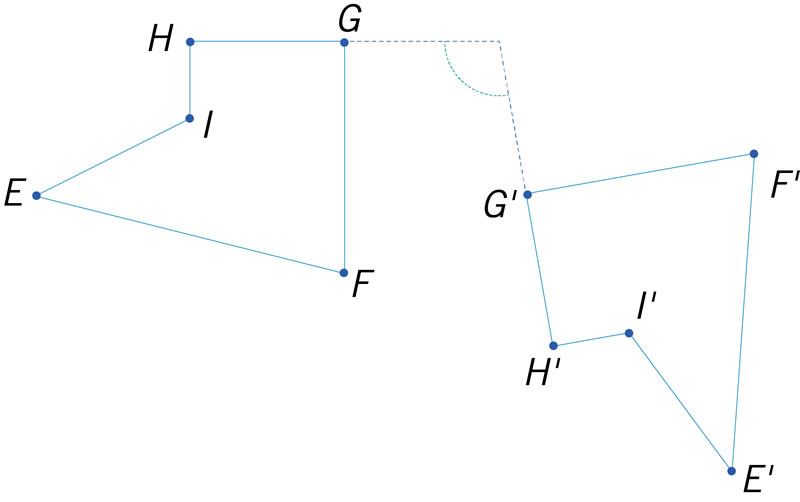
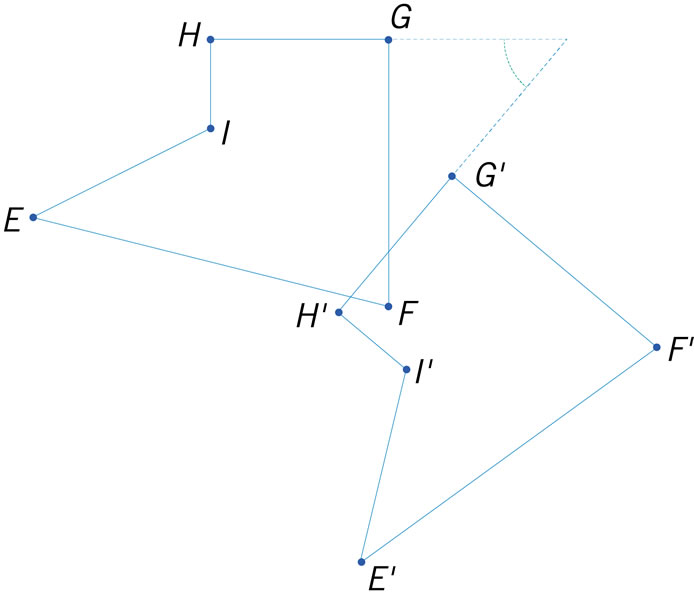
¿Qué figura representa una rotación de 50° del polígono EFGHI en el sentido antihorario?
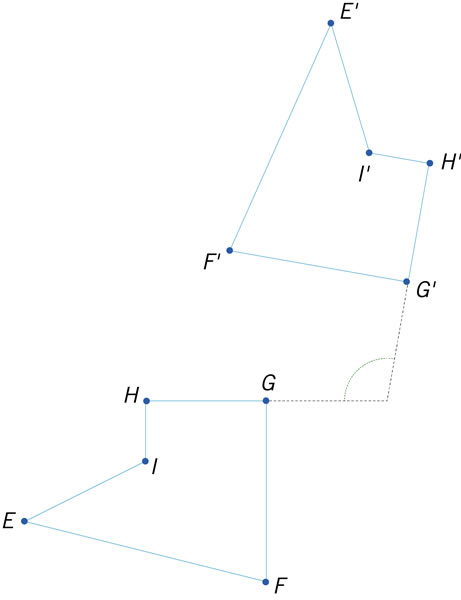
Al rotar una figura, trasladarla y rotarla nuevamente, la figura resultante tiene...
Dos rectas, l y m, son perpendiculares y una figura se reflejó con respecto a l y luego con respecto a m. ¿Con cuál de las transformaciones no es posible obtener el mismo resultado?
¿Cómo se obtuvo en esta figura el polígono W''X''Y''Z'' a partir del WXYZ?
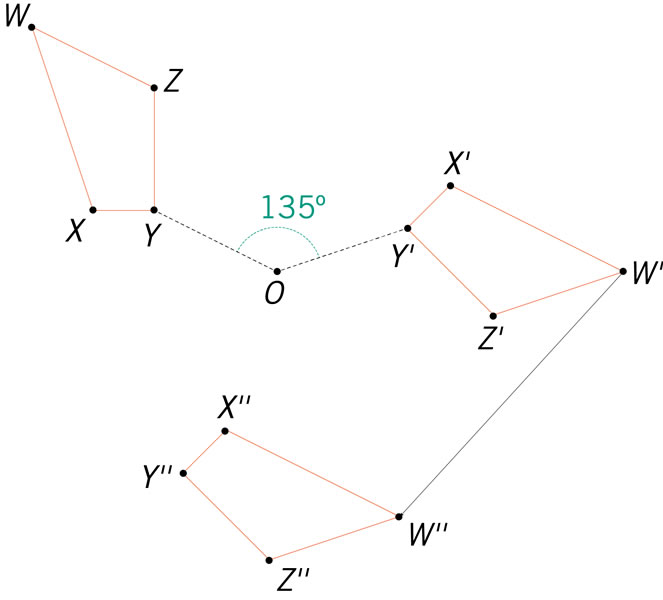
La figura muestra las medidas de las áreas de dos de los tres cuadrados construidos sobre los lados de un triángulo. ¿Cuál es la longitud del lado del cuadrado marcado con la letra x?
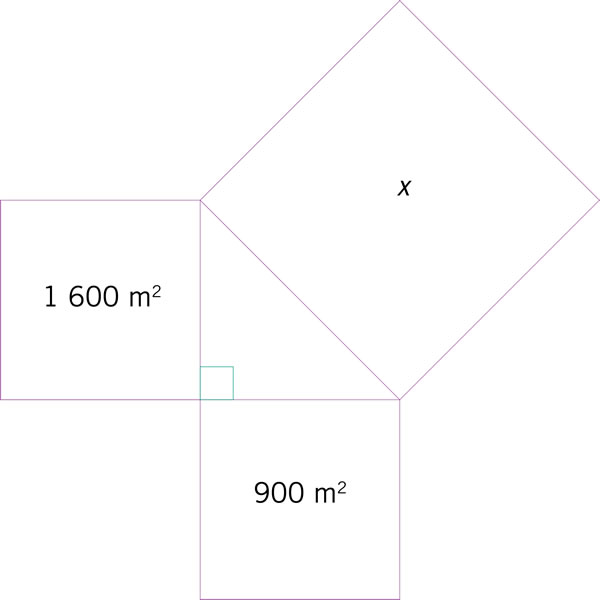
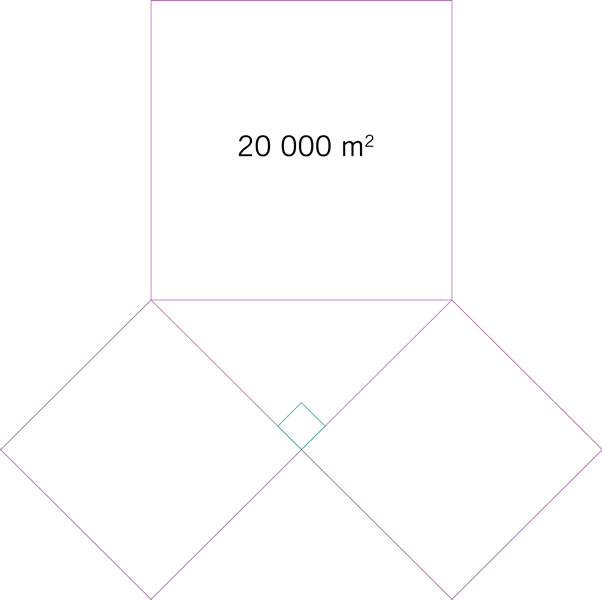
Los dos cuadrados pequeños de la siguiente figura son congruentes. ¿Cuál es la suma de sus áreas?
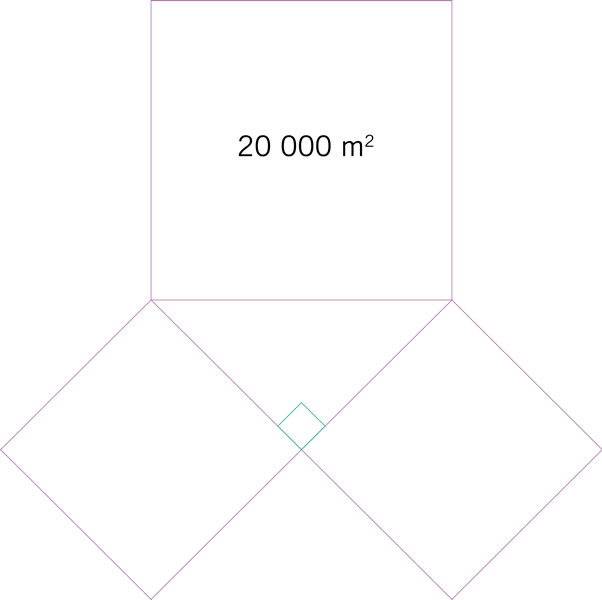
Los dos cuadrados pequeños de la siguiente figura son congruentes. ¿Cuál es la suma de sus perímetros?
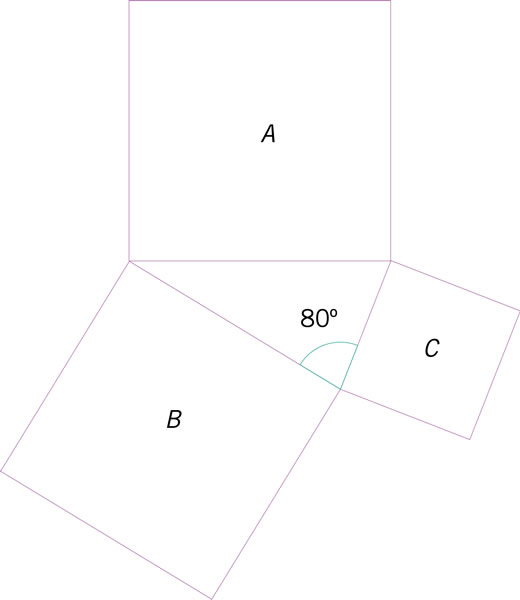
¿Cómo son entre sí el área del cuadrado A y la suma de las áreas de los cuadrados B y C?
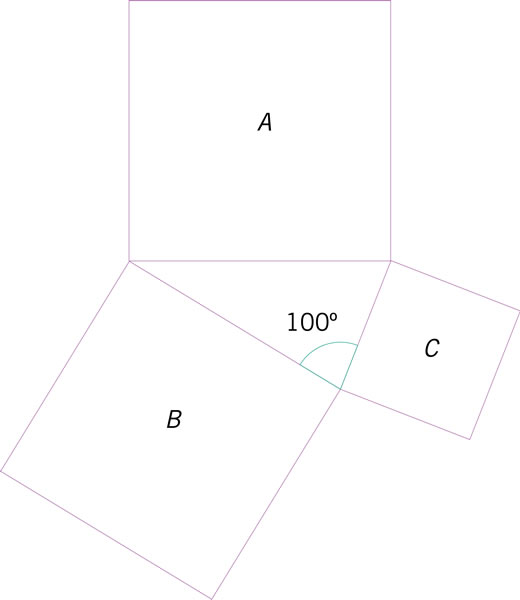
¿Cómo son entre sí el área del cuadrado A y la suma de las áreas de los cuadrados B y C?
El teorema de Pitágoras enuncia que...
Una escalera de 10 m tiene su base a 6 m de la pared. ¿Qué altura alcanza la escalera en la pared?
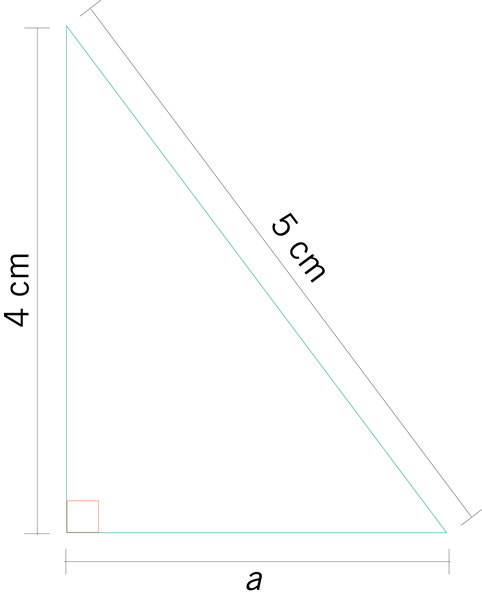
¿Cuál es el valor de a en el siguiente triángulo rectángulo?
En una urna hay 25 pelotas, algunas son azules y las demás, rojas. Si la probabilidad de tomar al azar una pelota azul es 0.48, ¿cuál es la probabilidad de tomar una pelota roja?
Se lanzan dos monedas al aire y al caer se consideran las caras superiores. Si la primera moneda fue sol y la segunda, águila, ¿cuál es la probabilidad de que suceda cualquier otro de los eventos posibles?
En la ruleta de una feria hay cuatro posibles resultados. La probabilidad de que el resultado sea "gana el doble" es de 20%, la probabilidad de que sea "pierde la mitad" es de \(\frac{1}{2}\) y la probabilidad de "pierde todo" es de 0.1. ¿Cuál es la probabilidad de obtener el cuarto resultado: "no pierde ni gana"?
En un experimento aleatorio hay cinco posibles resultados: A, B, C, D y E. La probabilidad de que el resultado sea A o B es de 0.2 y de que sea C, 0.65. Si los eventos D y E tienen la misma probabilidad de ocurrir, ¿cuál es la probabilidad de que el resultado sea D?
¿Cuál o cuáles son las soluciones de la ecuación x(x + 3) = 0?
Al transformar una figura, la directriz se utiliza para realizar...
Al rotar una figura 45° en cualquier sentido, y considerando su centro como centro de rotación, se obtuvo la misma figura y en la misma posición. ¿De cuál figura se trata?
¿Con cuál de las siguientes secuencias de transformaciones, un pentágono regular cambia de posición pero no de orientación?
¿Con cuál de las siguientes transformaciones se obtiene un bosquejo del símbolo de los juegos olímpicos modernos a partir de un anillo?
Sobre cada lado de un triángulo rectángulo se trazó un cuadrado, de modo que cada lado del triángulo es el lado de un cuadrado. Los cuadrados que están sobre los lados más pequeños del triángulo tienen, respectivamente, 25 y 144 cuadros, todos del mismo tamaño. ¿Cuántos cuadros del mismo tamaño tendrá el tercer cuadrado?
Sobre cada lado de un triángulo rectángulo se trazó un cuadrado, de modo que cada lado del triángulo es el lado de un cuadrado. Si uno de los lados del triángulo mide a unidades y el área del cuadrado que se formó sobre el lado más grande del triángulo es de 5a2, ¿cuál es la medida del tercer lado del triángulo?
La hipotenusa de un triángulo rectángulo mide 3.5 unidades y uno de sus catetos, 2.8 unidades. ¿Cuál es la medida del otro cateto?
En una calle hay tres postes: el poste A está en una acera y los postes B y C, en la acera de enfrente. Los tres postes juntos forman un triángulo rectángulo. La distancia entre los postes A y B es de 6.8 m y la distancia entre los postes B y C es de 4 m. ¿Cuál es la distancia entre los postes A y C, si ésta es mayor que las demás?
En una urna hay 3 canicas azules, 6 verdes y algunas amarillas. Si Luis elige una canica al azar, la probabilidad de que sea azul o de que sea amarilla es de \(\frac{8}{14}\). ¿Cuántas canicas amarillas hay en la urna?
Dada la ecuación \(10x + 5{x^2} = 2\), ¿cuál es la situación correcta de sus coeficientes en la fórmula?
En la fórmula general para resolver ecuaciones de segundo grado, hay dos soluciones, en los números reales, cuando:
¿Cuál de las siguientes ecuaciones de segundo grado no tiene solución en los números reales?
¿Qué valores de x satisfacen la ecuación 3x2 – 4x + 1 = 0?
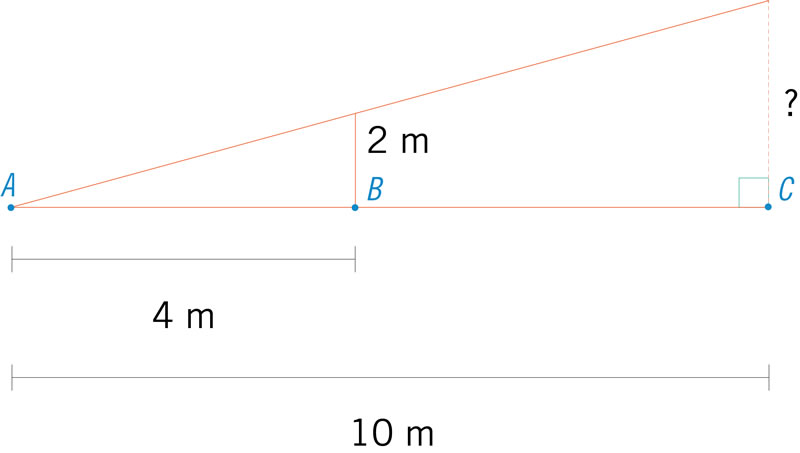
Calcula el valor del segmento marcado con signo de interrogación.
Un marinero de pie, en la proa de un velero, observa un faro en la costa. Si la estatua del marinero es de 1.7 m, proyecta una sombra de 2 m de largo sobre el piso del velero y el extremo de la sombra del faro llega exactamente hasta la proa, ¿qué distancia le falta recorrer al velero para llegar a la costa? La altura del faro es de 30 m.
¿Cuál es el perímetro de la siguiente figura si todos los triángulos son semejantes?
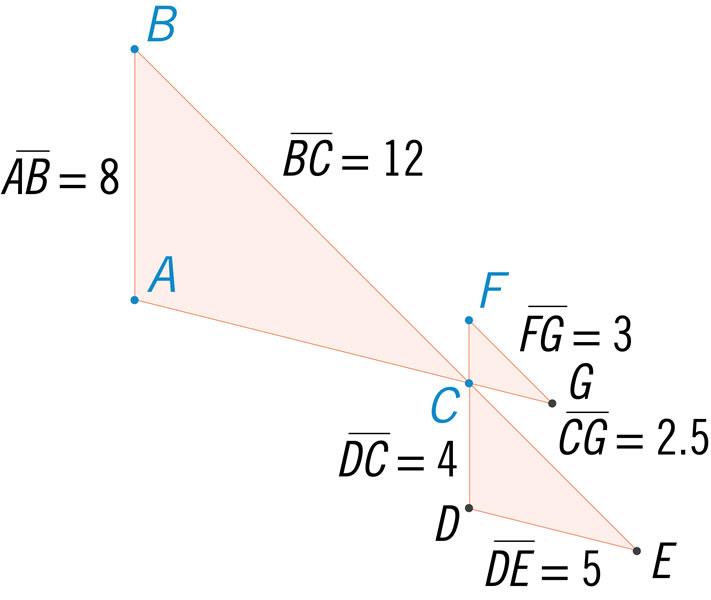
El enunciado: "Dos rectas paralelas que cortan a otras dos rectas generan segmentos proporcionales", corresponde a:
Calcula la longitud del segmento \(\overline {LM} \), considerando que las rectas s, t y w son paralelas.
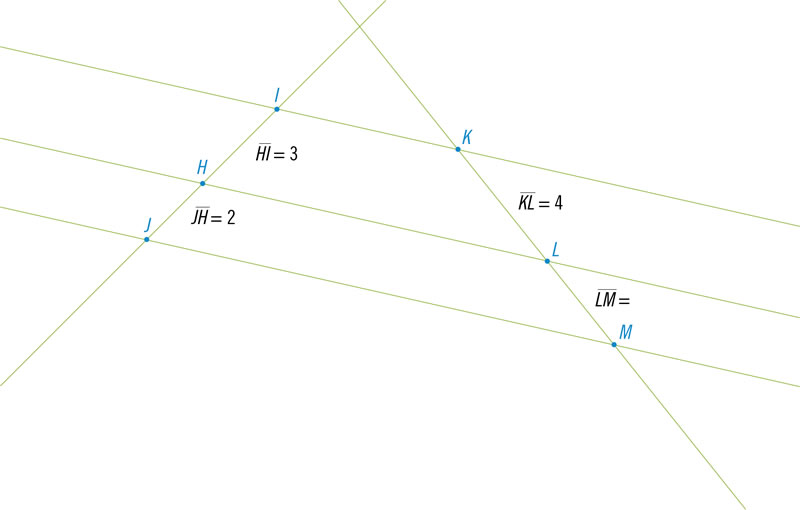
Calcula el valor de la distancia del segmento \(\overline {AC} \).
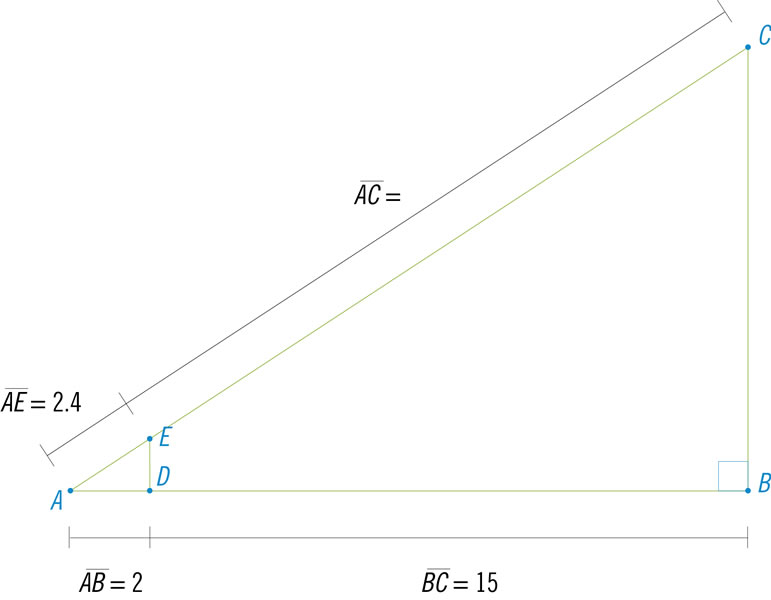
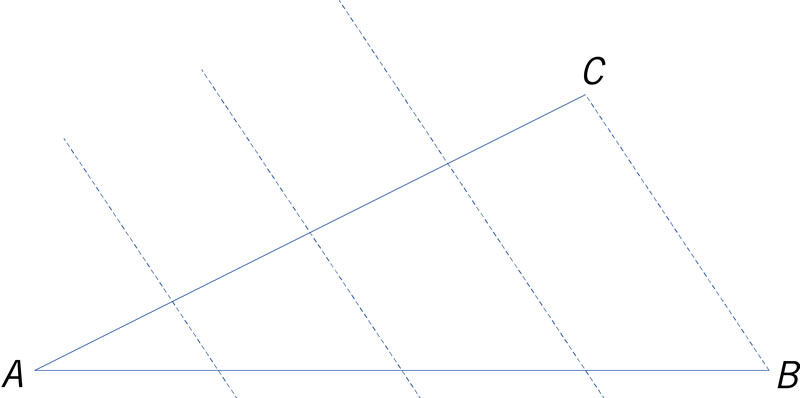
El segmento AB está dividido en 4 partes y se desea dividir el segmento AC también en 4 partes. Para ello se trazan rectas paralelas al segmento CB que pasan por las líneas divisorias del segmento AB. ¿Qué teorema o principio justifica este procedimiento?
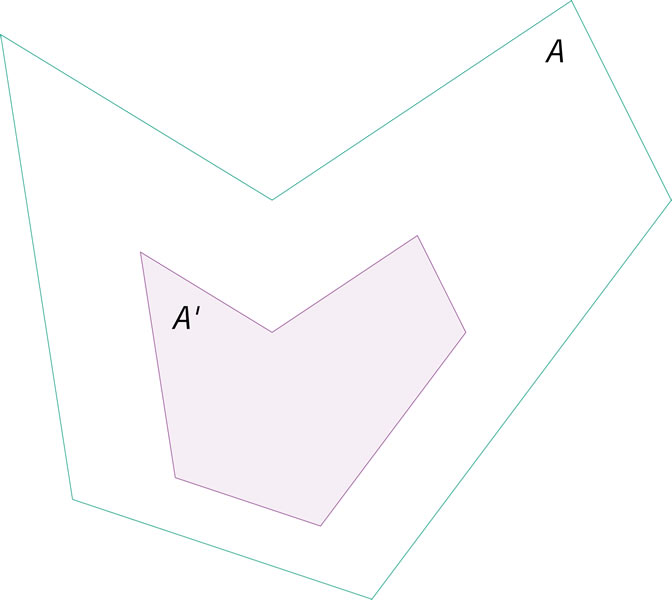
¿Cómo es la figura homotética respecto a la original cuando la razón de homotecia es menor que 1 pero mayor que 0?
¿Cómo es la figura homotética respecto a la original cuando la razón de homotecia es negativa?
¿Dónde se encuentra el centro de homotecia entre las siguientes figuras?
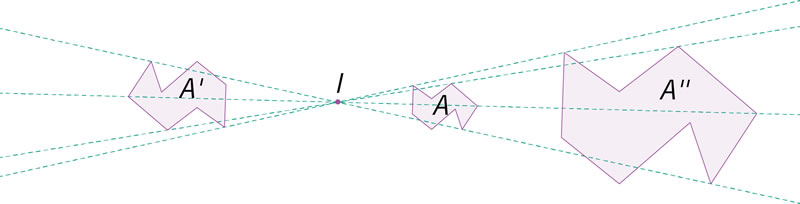
La razón de homotecia entre las figuras A y A’ es –1.5 y entre A’ y A’’ es –2. ¿Cuál es la razón de homotecia entre las figuras A y A’’?
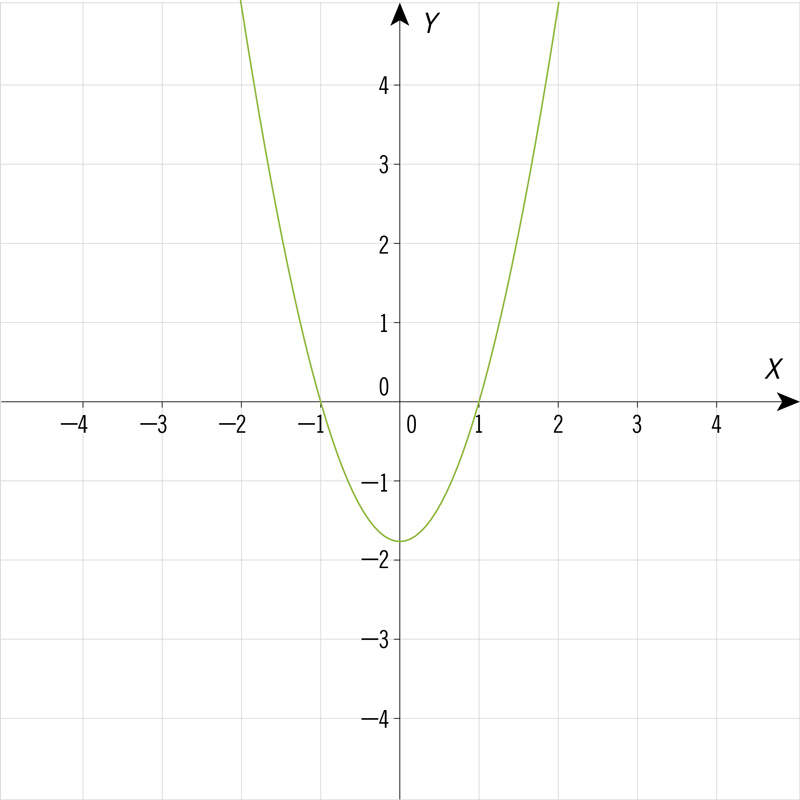
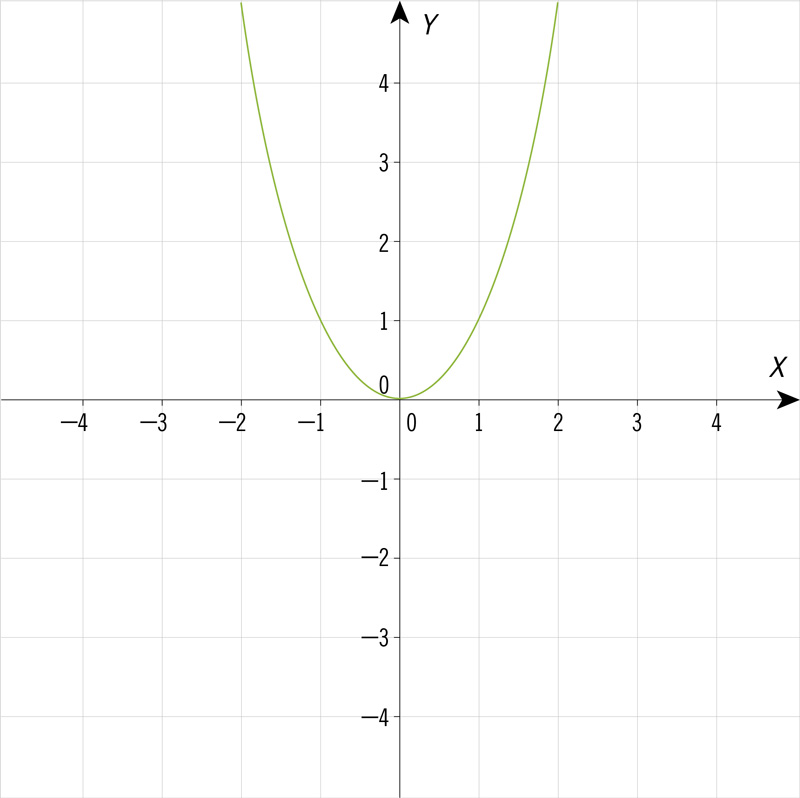
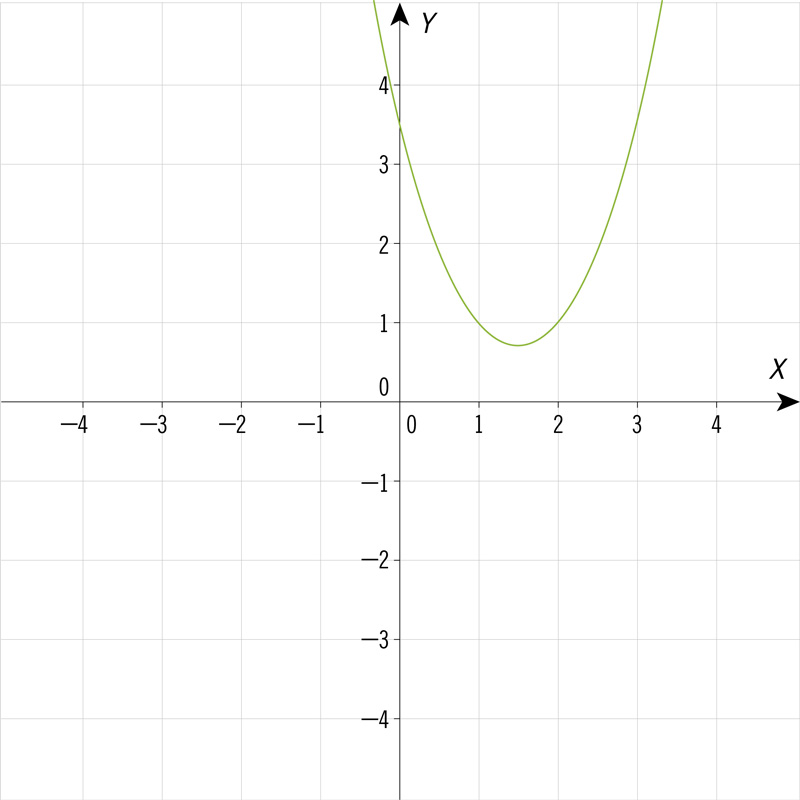
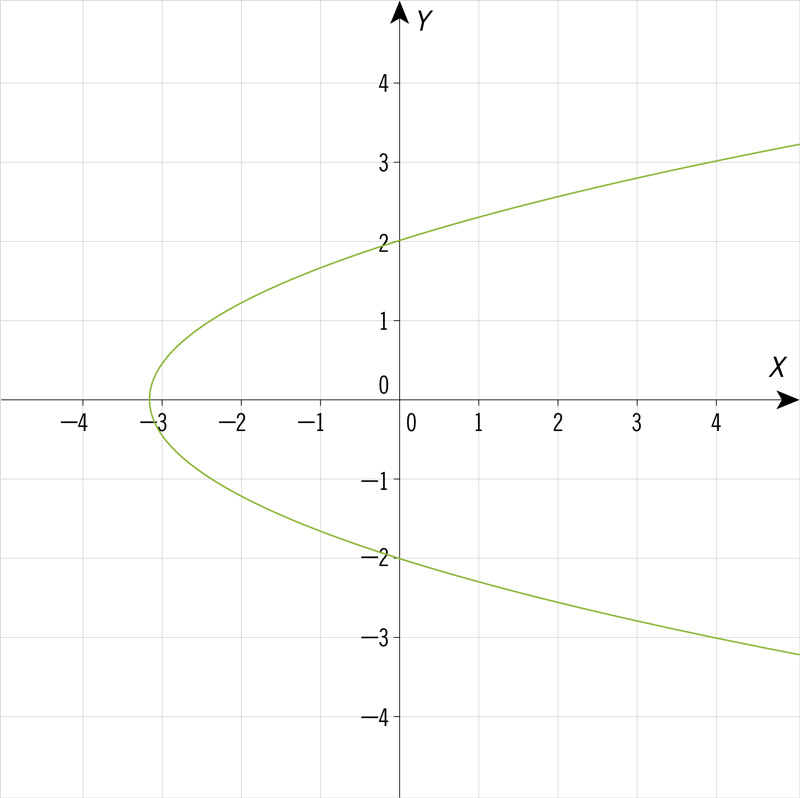
¿Cuál de las siguientes gráficas corresponde a una ecuación cuadrática de la forma \(y = a{x^2} + bx + c\), con dos soluciones cuando la variable \(y\) es igual a 0?
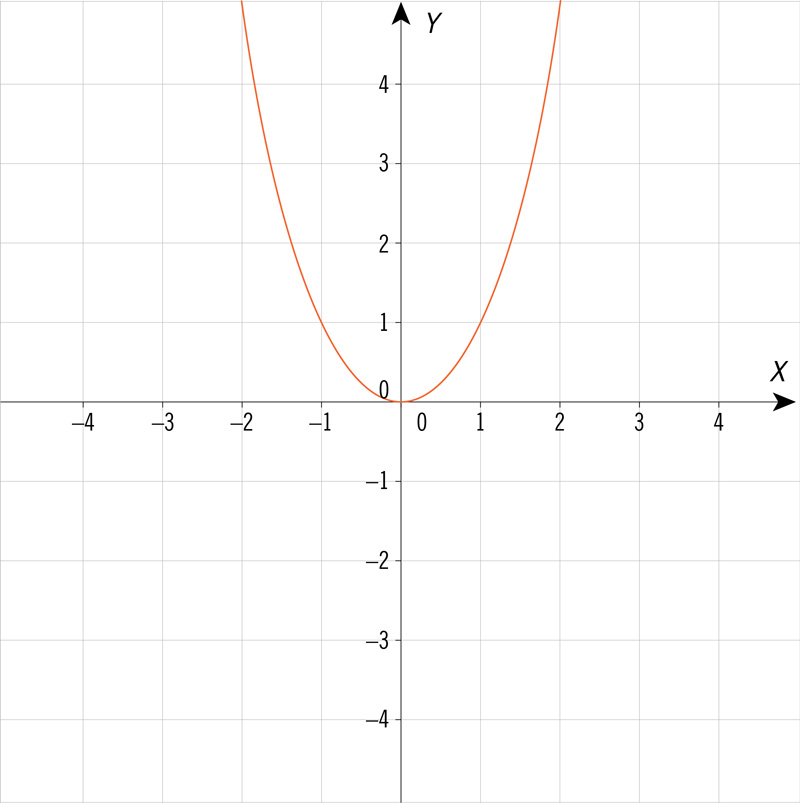
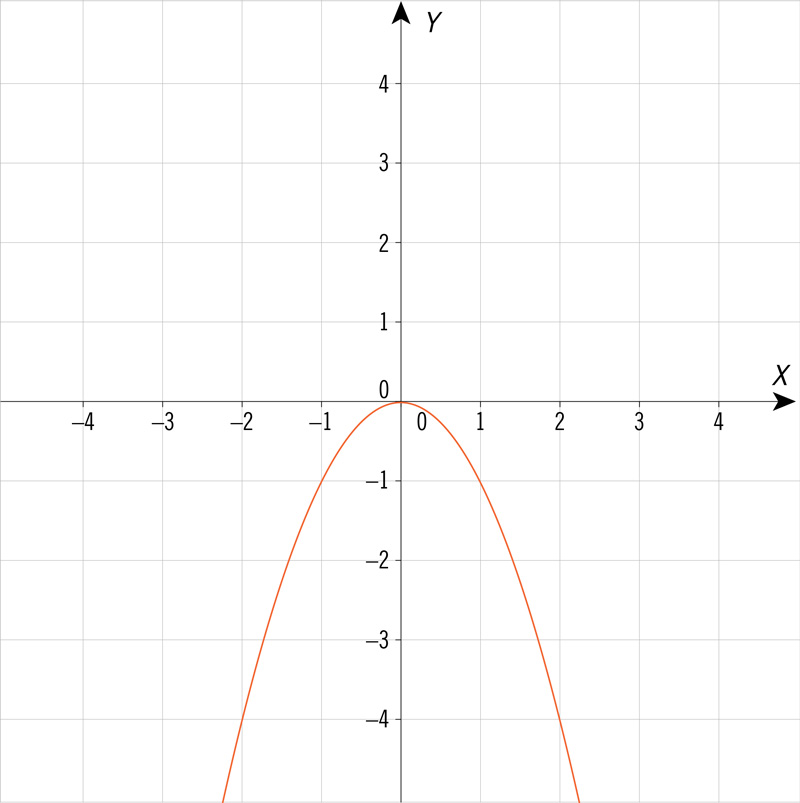
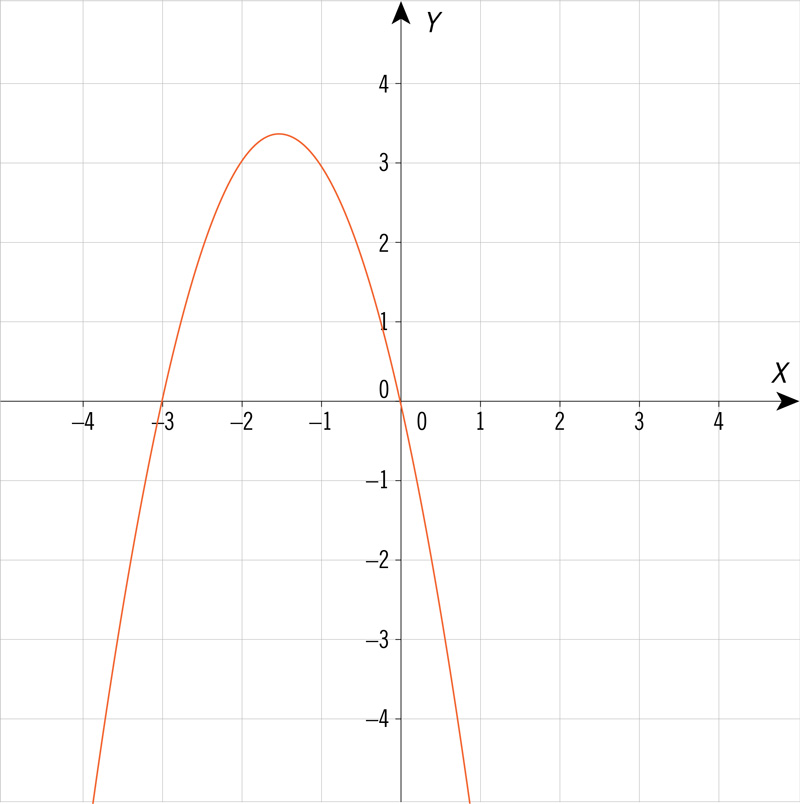
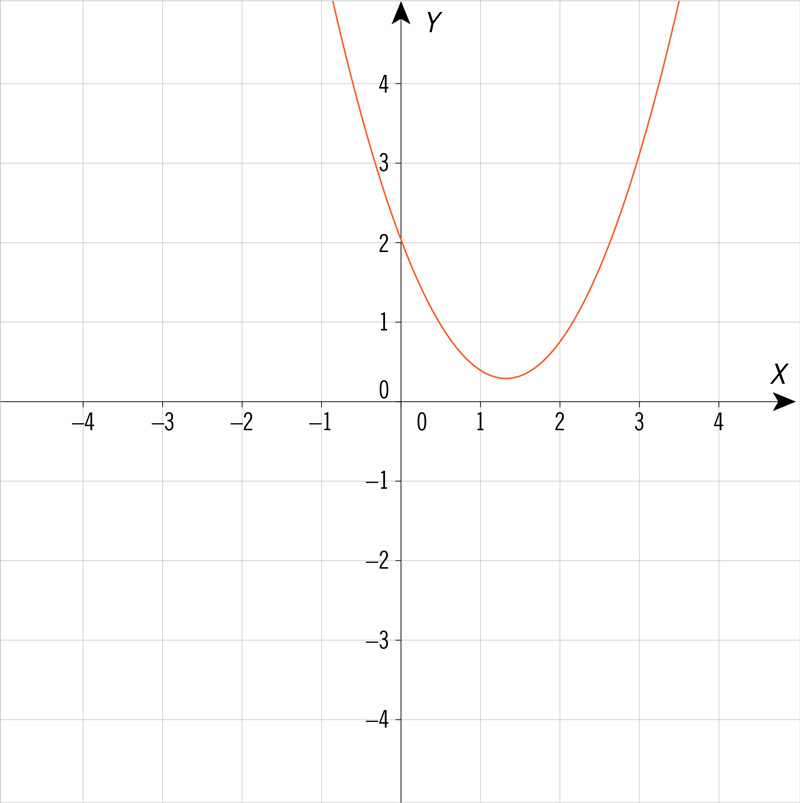
¿Qué gráfica corresponde a los valores de la tabla siguiente?
| X | –3 | –2 | –1 | 0 | 1 | 2 |
| Y | 17 | 7 | 1 | –1 | 1 | 7 |
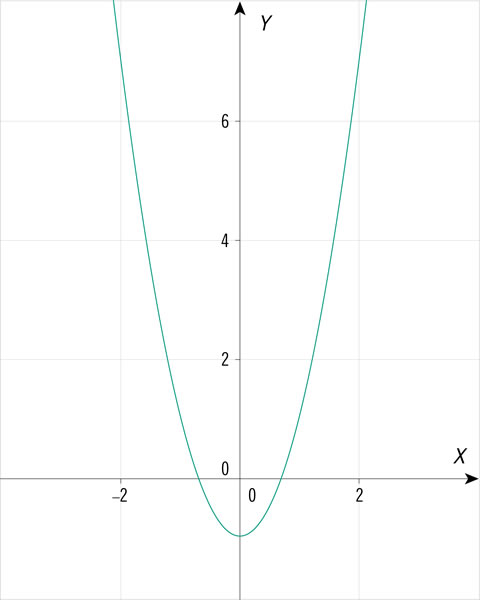
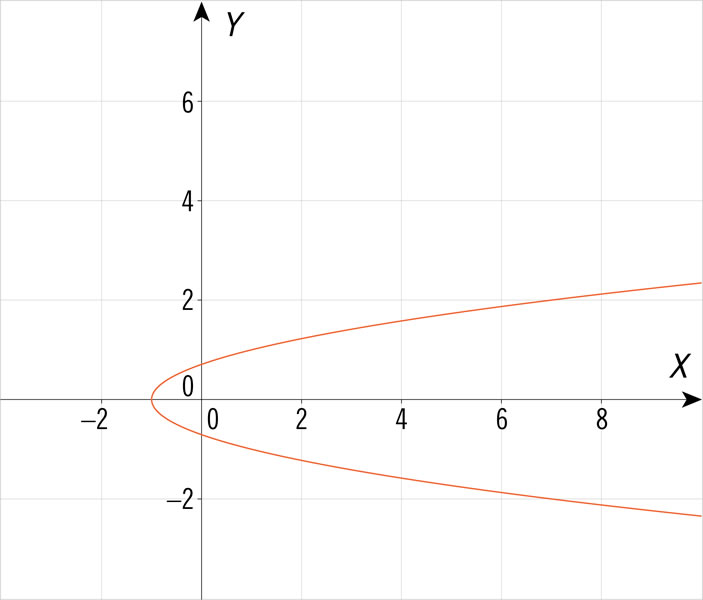
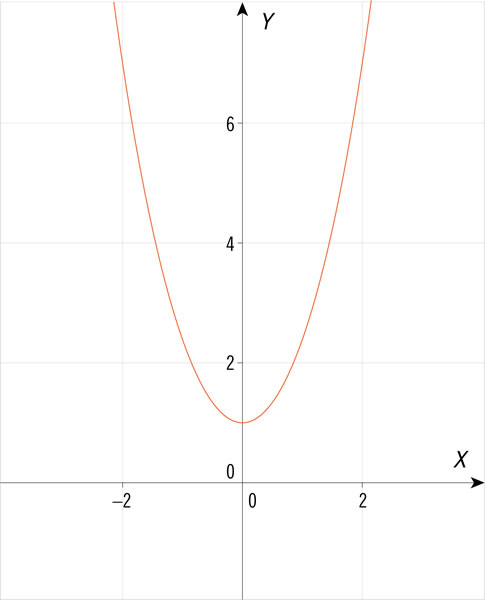
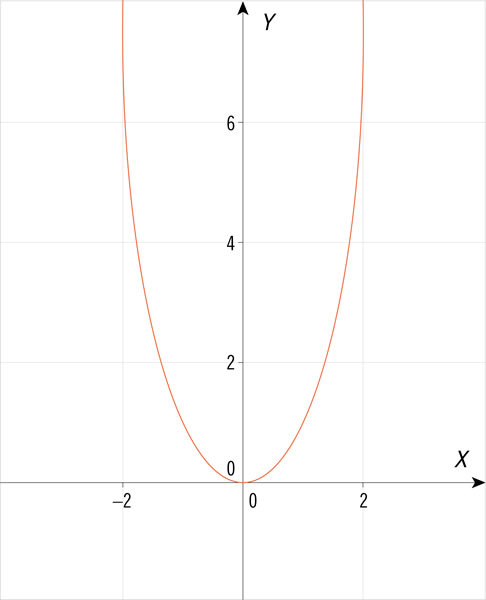
¿Qué gráfica representa una ecuación cuadrática con una sola solución?
De acuerdo con la gráfica, ¿cómo varió el precio del dólar en las últimas cuatro horas?
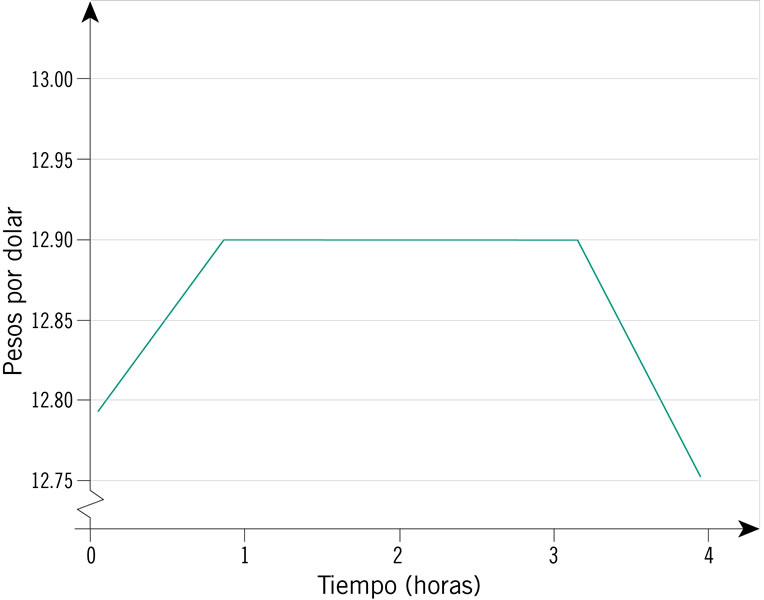
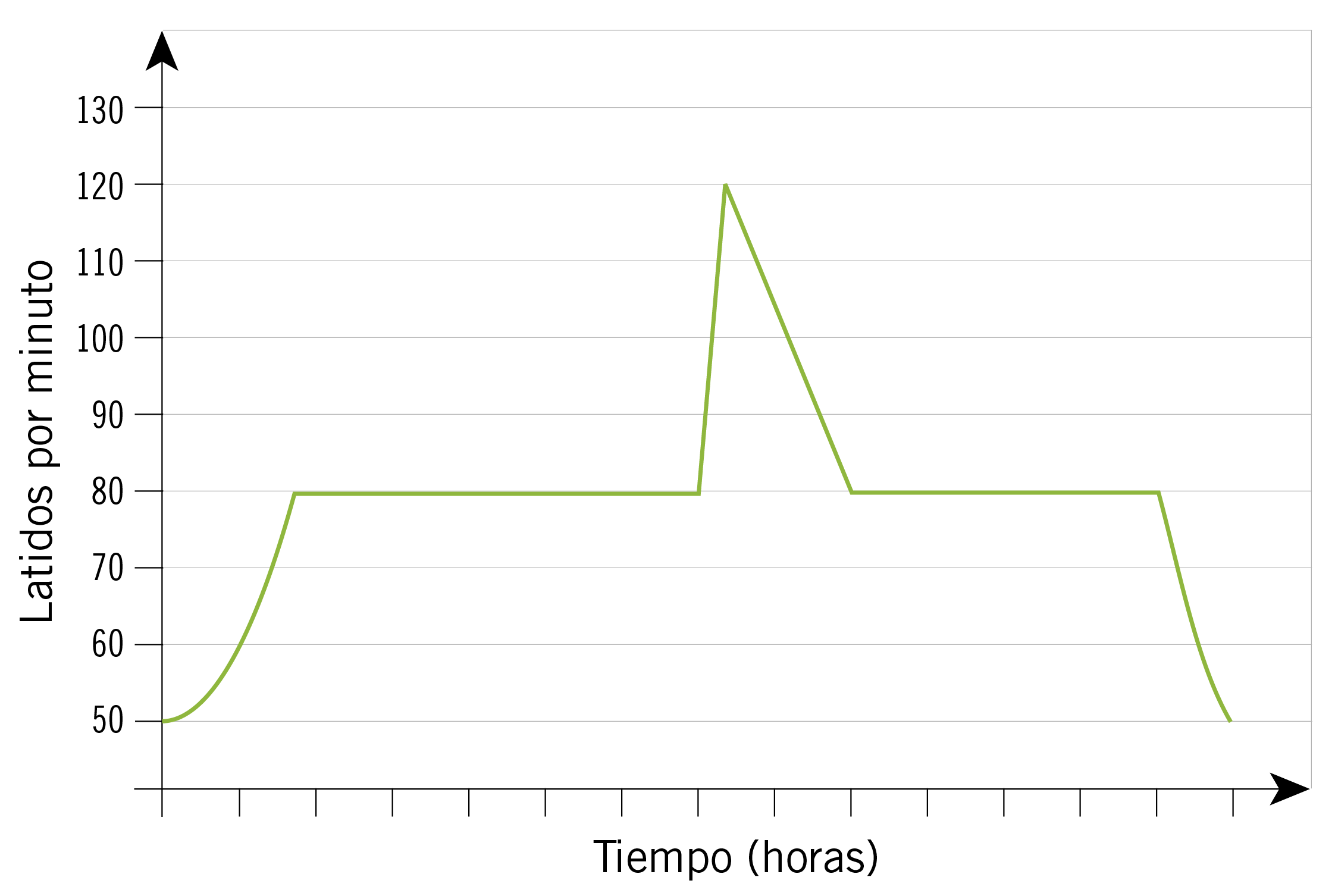
A lo largo de un día se observó el ritmo cardiaco de una persona: desde que despertó hasta que se durmió. Al iniciar el día su ritmo se incrementó de manera paulatina, pero no constante, hasta que se estabilizó. Así se mantuvo varias horas hasta después de realizar ejercicio físico que se incrementó rápida y constantemente, pero luego disminuyó en forma constante hasta normalizarse. Al final del día, antes de dormir, su ritmo disminuyó de nuevo, pero de manera no constante hasta estabilizarse. ¿Qué gráfica representa la situación descrita?
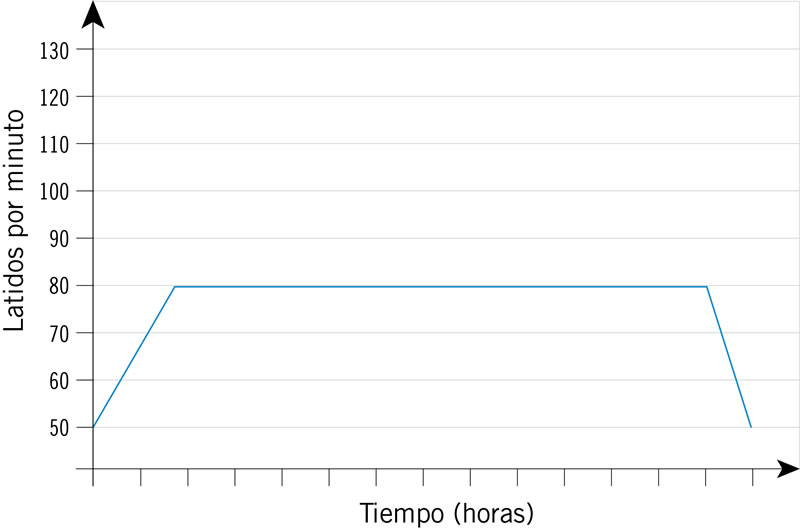
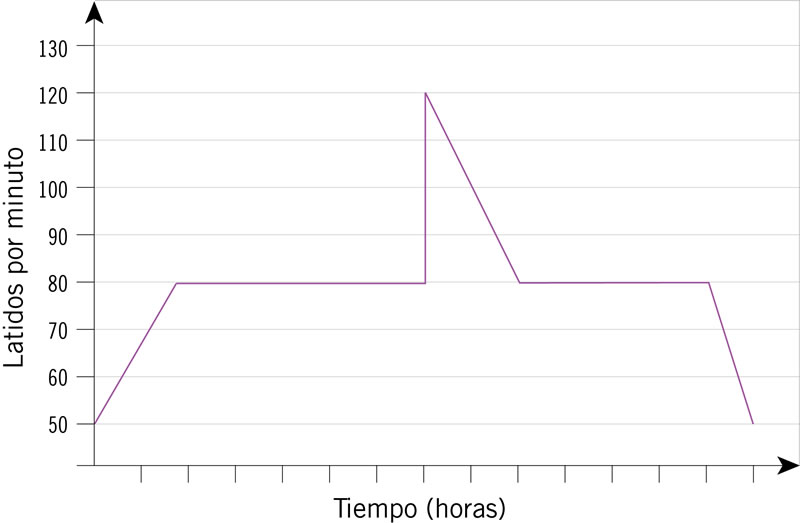
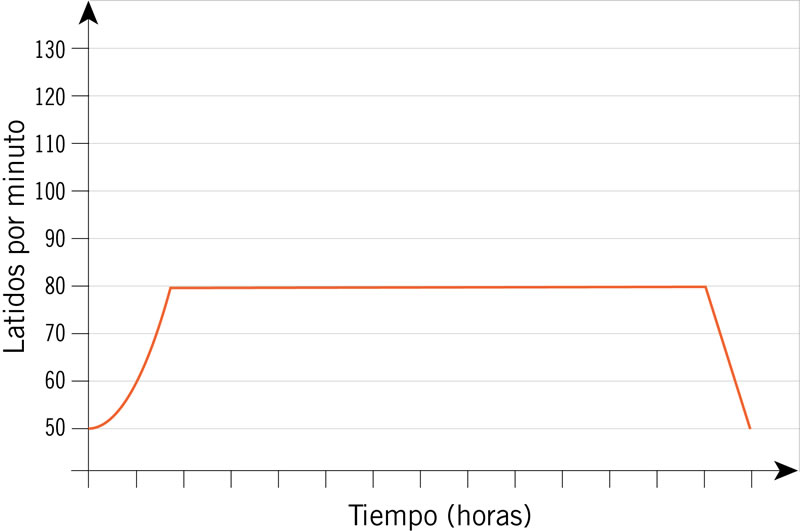
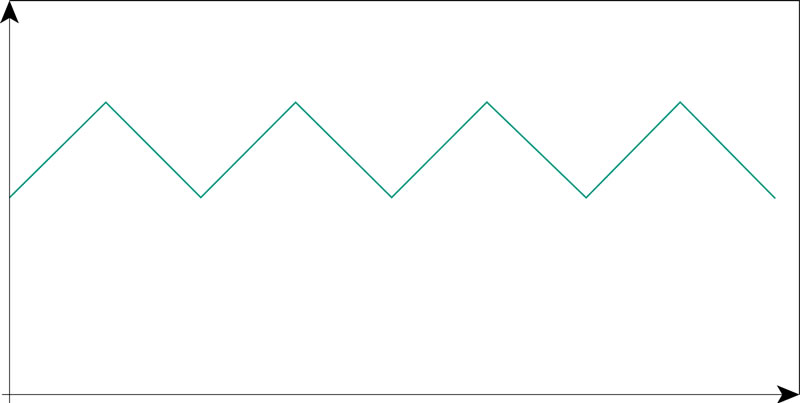
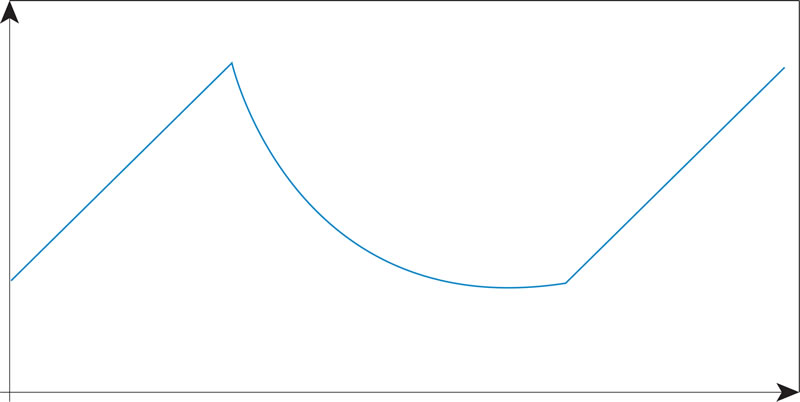
¿Qué gráfica representa el movimiento de una boya al paso de un tren de ondas en la superficie del agua?


¿Cuál es la probabilidad de que al lanzar dos dados, cuyas caras están numeradas del 1 al 6, al caer la cara superior del primero muestre el número 4 y la del segundo el número 6?
La probabilidad de que hoy se suspendan las clases es de 0.36 y de que esté lloviendo es de 0.4. ¿Cuál es la probabilidad de que no haya clases y llueva?
En cada mazo con 52 cartas sólo hay un dos de diamantes. Si se tienen dos mazos, ¿cuál es la probabilidad de sacar en cada mazo un dos de diamantes?
A dos personas se les hizo una pregunta y la probabilidad de que acierten es de 0.12. ¿Cuál es la probabilidad de que ambas personas se equivoquen?
¿Cuántas soluciones en los números reales tiene la ecuación x2 − 4x + 6 = 0?
Las soluciones de la ecuación (x − 1)(x + 1) = 16 son:
¿Cuáles de los siguientes tipos de triángulos necesariamente son triángulos semejantes?
Al trazar la diagonal mayor de un romboide se obtienen triángulos congruentes. ¿Cuál de los siguientes criterios justifica la afirmación anterior?
¿Cuál es la longitud del segmento \(\overline{EB}\) de la siguiente figura?
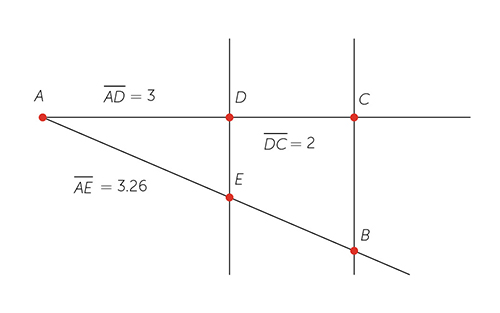
¿Qué situación se puede resolver mediante el teorema de Tales?
Cualesquiera dos figuras son homotéticas entre sí...
Al graficar la fórmula para calcular el área de un círculo, A = π × r2, la variable r se representó en el eje horizontal y la variable A, en el vertical. ¿Cuál es la forma de la gráfica?
La gráfica de la distancia que recorre un automóvil en términos del tiempo transcurrido se compone por tres secciones: la primera es una línea curva cuyo valor aumenta de izquierda a derecha; la segunda, una línea recta cuyo valor aumenta de izquierda a derecha; la tercera, una recta horizontal. ¿Cuál enunciado describe la velocidad del automóvil?
Pablo se dirige a casa de Jorge. En el camino, entre sus casas, hay una trifurcación y cada uno de los caminos de la trifurcación tiene una bifurcación; es decir, primero el camino se divide en tres y después cada uno de los caminos se divide en dos. Si sólo uno de los posibles caminos llega a casa de Jorge, ¿cuál es la probabilidad de que Pablo elija al azar el camino correcto?
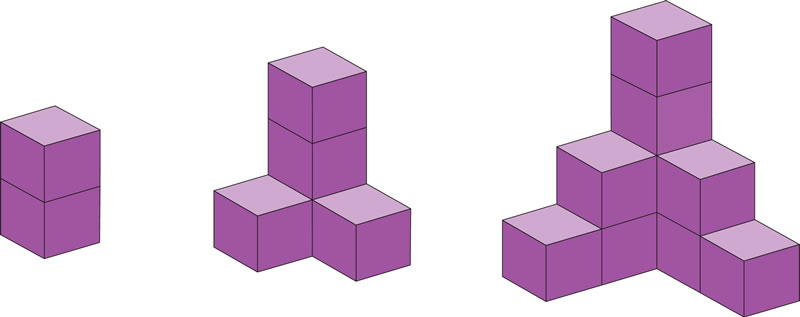
¿Qué expresión algebraica corresponde a la cantidad de cubos de la enésima figura de la siguiente sucesión?
¿Cuál de las siguientes expresiones algebraicas es la regla de correspondencia de la sucesión: 3, 6, 11, 18, 27?
¿Qué número pertenece a la sucesión con expresión x2 + 2x?
¿Cuál es la generatriz del sólido de revolución que se forma al girar el triángulo en torno al segmento a?
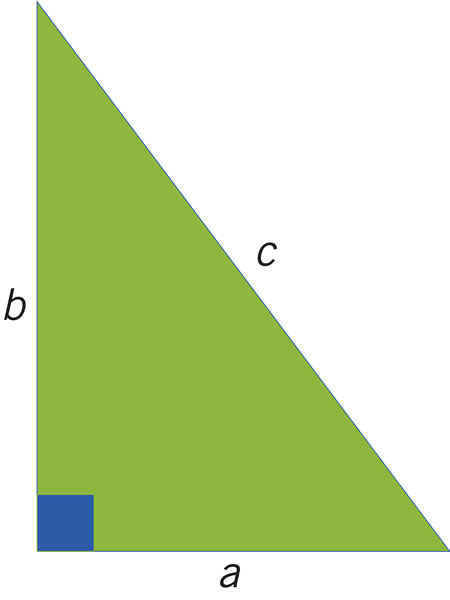
¿Cuál de estas figuras planas genera un cono truncado al girar en torno a uno de sus lados?




¿Cuánto mide la circunferencia de la base del cilindro que se forma al rotar el rectángulo sobre el eje que se indica?
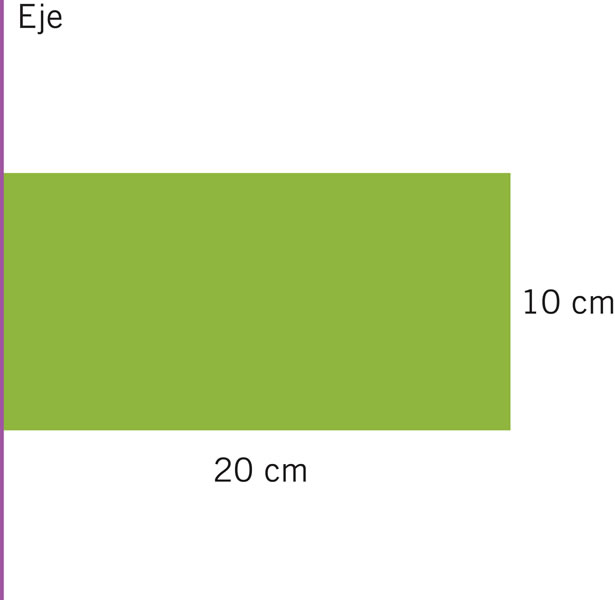
¿Cuál es el valor de la pendiente de la recta que pasa por los puntos A y C?
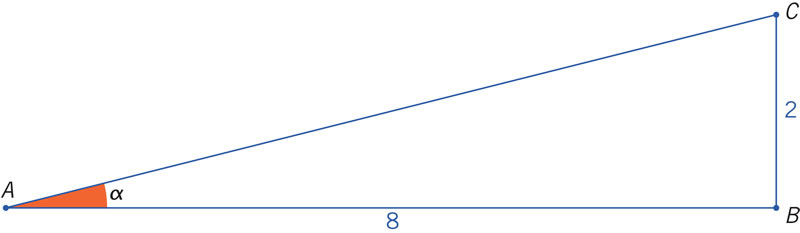
¿Cuánto mide el ángulo que se forma entre la horizontal y la recta?
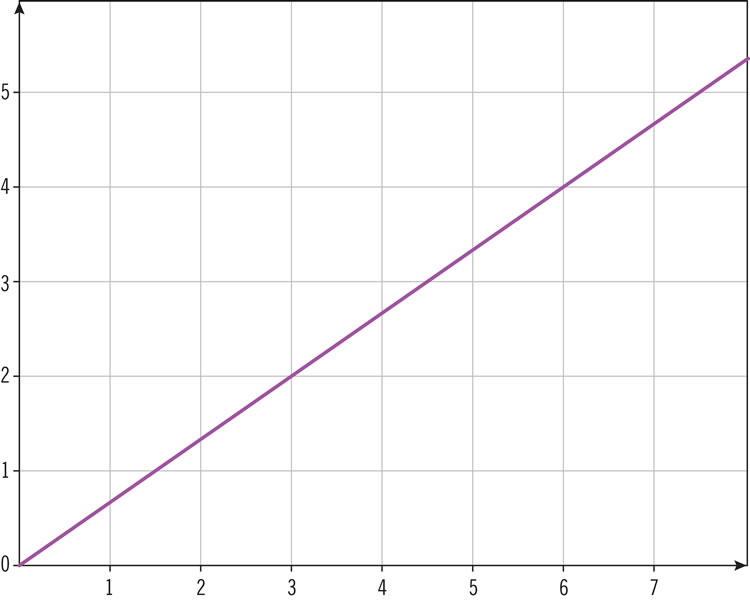
Si la pendiente de una recta es de 2.5, ¿qué oración es verdadera?
¿En cuál de estas gráficas el ángulo que forman la horizontal y la recta mide 38.66°?
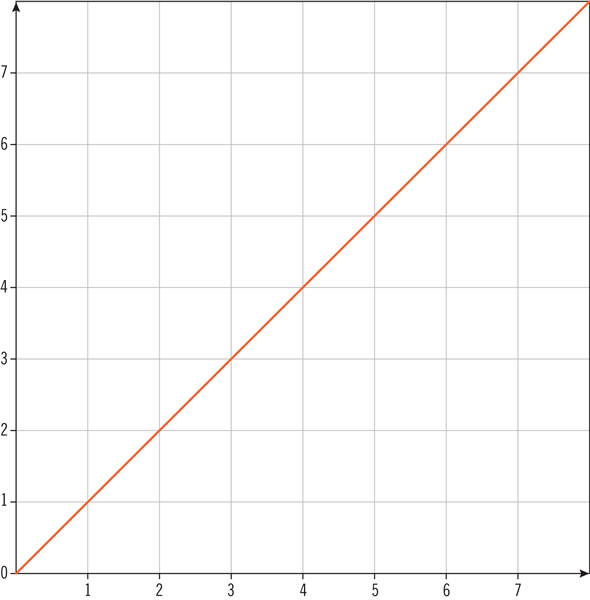
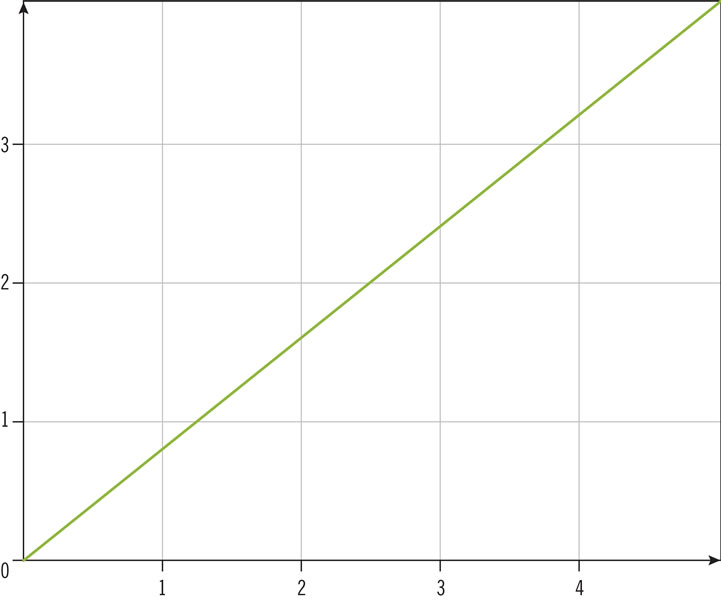
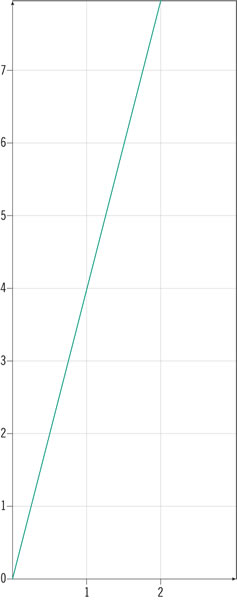
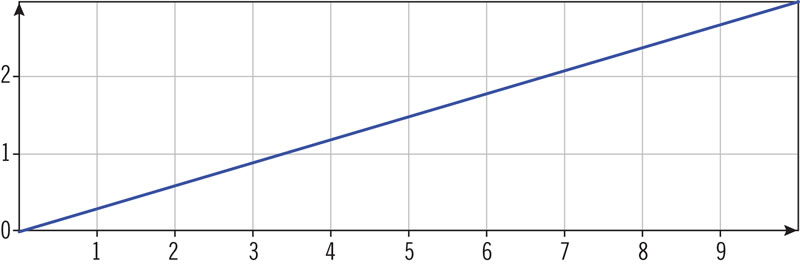
Observa el triángulo rectángulo. ¿Cuál es el valor del coseno de los ángulos α y β?
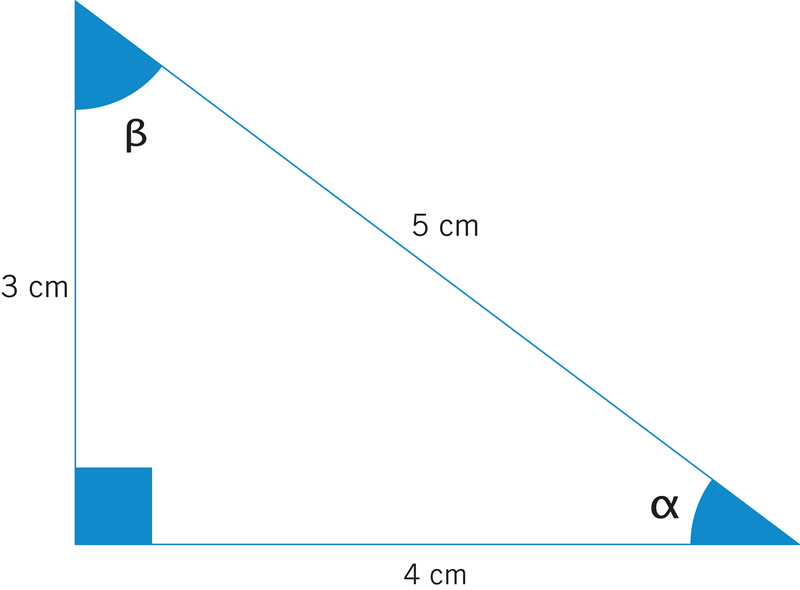
El valor de la hipotenusa del siguiente triángulo se calcula directamente con...

La razón entre el cateto opuesto al ángulo y la hipotenusa en dos triángulos rectángulos es la misma si...
Conforme el valor de un ángulo se acerca a 90°, el valor del seno...
Conforme el valor de un ángulo se acerca a 90°, el valor de la tangente...
Si en un triángulo rectángulo sus ángulos interiores A y B son agudos, y el valor del coseno del ángulo A es menor que el valor del coseno del ángulo B, entonces...
Si los ángulos internos x y y en un triángulo rectángulo cumplen que x + y = 90°, con x, y ≠ 0, ¿cuál de las siguientes oraciones es la verdadera?
En la entrada de una escuela se va a construir una rampa para personas con discapacidad. De acuerdo con la norma establecida, su altura debe medir 6% del largo de su base. La siguiente imagen muestra un diagrama de la rampa. Si el largo de su base, que en la imagen se indica como un segmento punteado, debe ser de 180 cm, ¿cuál es el ángulo de inclinación y la longitud de la rampa?

Observa las siguientes gráficas. ¿En cuál es mayor la razón de cambio?
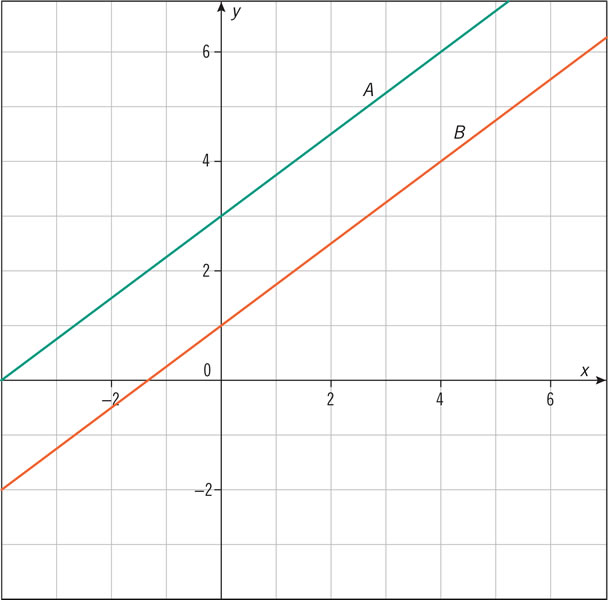
Observa las gráficas. ¿En cuál es mayor la razón de cambio?
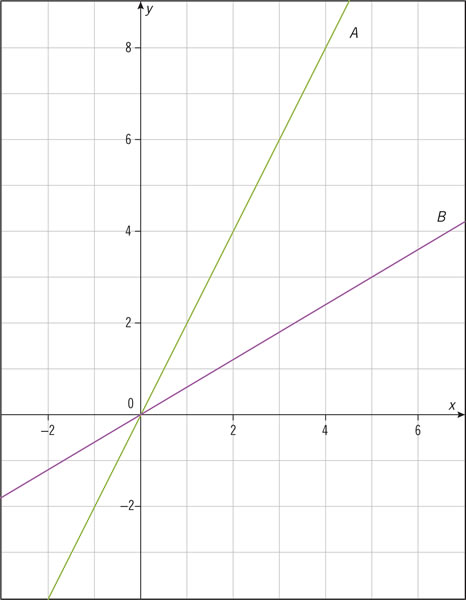
A continuación se muestra la gráfica de una función lineal. ¿Cuál es la razón de cambio?
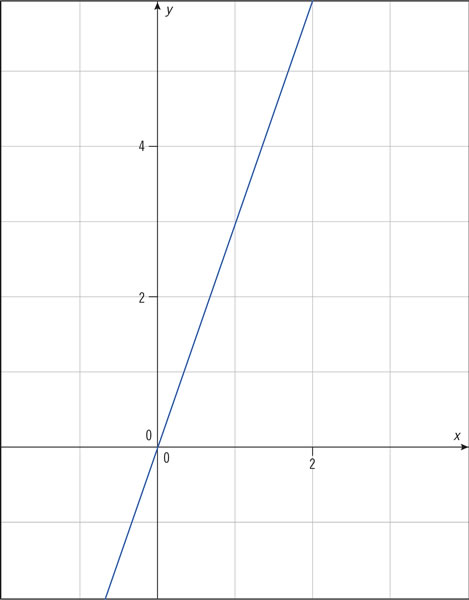
Si en una función lineal la razón de cambio es negativa y la gráfica que la representa es una recta que pasa por el origen, entonces...
¿Qué conjunto de datos está más disperso?
¿Cuál de los siguientes conjuntos de datos tiene un rango menor?
¿Cuál es la desviación media del conjunto 7, 8, 4, 5, 6, 8, 4?
¿Cuál de las siguientes expresiones corresponde con la sucesión −5, −20, −45, −80,...?
¿Qué número no pertenece a la sucesión definida por la expresión 2n2 + 4n?
¿Cuáles de los siguientes datos no son suficientes para trazar un único desarrollo plano de un cono?
En una recta que pasa por el origen de un plano cartesiano se trazó un triángulo rectángulo de tal modo que su hipotenusa es un segmento sobre la recta. Además, uno de sus catetos es horizontal y mide 1.2 cm y el otro cateto es vertical y mide 1.6 cm. ¿Cuánto mide el ángulo que forma la recta con el eje horizontal?
Los ángulos agudos de un triángulo rectángulo son los ángulos A y B. Si cos A = 0.819 y cos B = 0.574, ¿cuánto vale sen B?
En el círculo unitario, conforme la medida de un ángulo aumenta de 0° a 90°, ¿qué sucede con el valor de la tangente?
Si uno de los ángulos agudos de un triángulo rectángulo mide 35° y el cateto opuesto a ese ángulo mide 10 unidades, ¿cuántas unidades mide la hipotenusa?
Santiago produce desinfectante para verduras. El lunes, antes de iniciar su jornada laboral, tenía 10 cajas de desinfectante y el viernes, al terminar la jornada laboral, tenía 70 cajas. Si esa semana no vendió caja alguna, ¿cuál es la razón de cambio que representa la cantidad de cajas que produce por día?
¿Cuáles son el rango y la desviación media del conjunto de datos 5, 6, 7, 4, 5?
¿Cuál es la forma del histograma de un conjunto de datos en los que los datos son parecidos al promedio y cómo es el valor de la desviación media?
Jimena vende jugos a $8.00 y licuados a $12.00. Si le compran 20 productos y sus ingresos son de $208.00, ¿cuántos jugos vendió?
Si a cinco veces el mayor de dos números (M) se añade siete veces el número menor (m), la suma es 316, y si a nueve veces el menor se resta el cuádruplo del mayor, la diferencia es 83. ¿Cuáles son los números?
Si dos paletas más tres helados cuestan $22.00, y cuatro paletas más seis helados valen $44.00, ¿cuál es el precio de cada paleta y de cada helado?
El cuadrado de un número más dos veces el mismo número menos siete es igual ocho. ¿De qué número o números se trata?
Un número al cuadrado más el mismo número más uno es igual a cero. ¿Cuál es ese número?
¿Cómo se llama la cónica que se obtiene con un corte como el que muestra la figura siguiente?
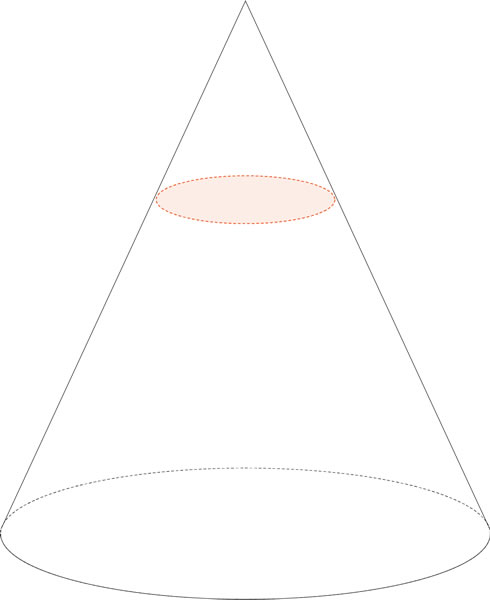
¿Qué nombre recibe la cónica que resulta de un corte como el que se ilustra en esta figura?
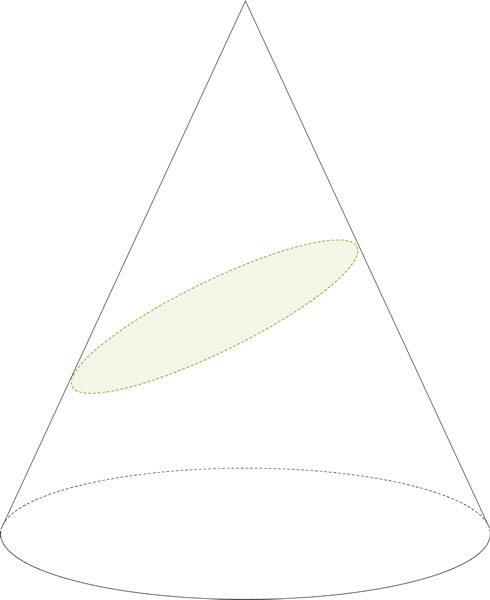
¿Cómo se llama la cónica que se obtiene con un corte como el que muestra la figura siguiente?
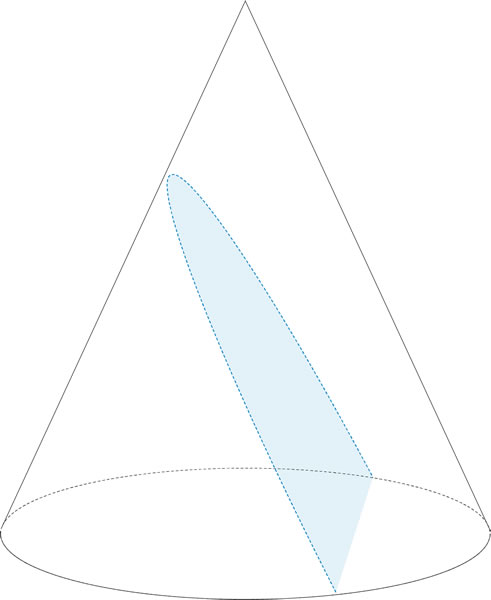
¿Cómo se llama la cónica que resulta de un corte como el que ilustra la figura?
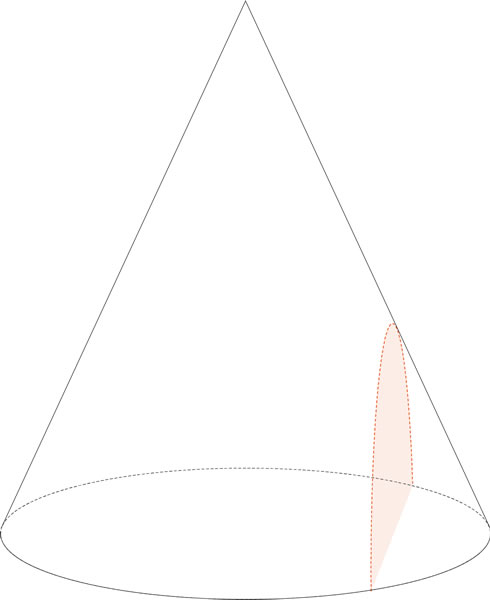
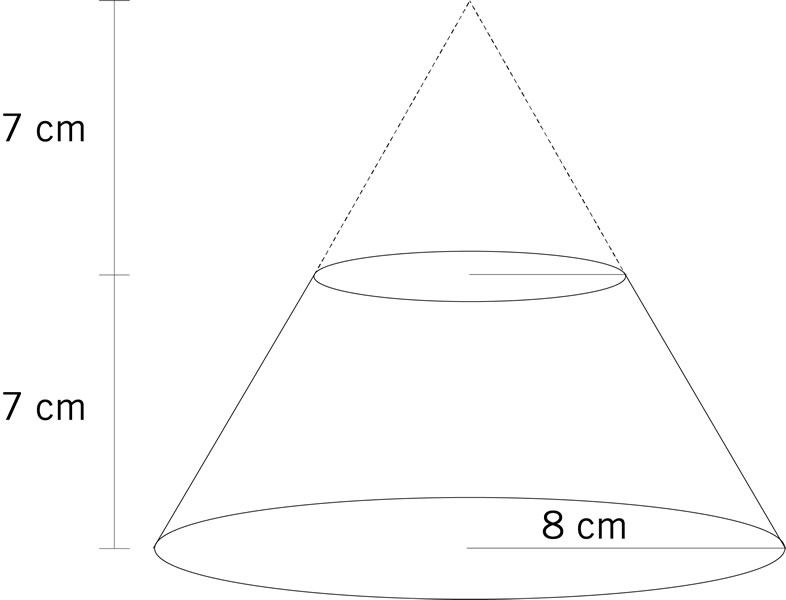
Si la altura del cono completo de esta figura es de 7 cm, ¿cuál es el radio del cono más pequeño?
¿Cuál es la fórmula para obtener el volumen de un cilindro de altura h y radio r?
¿Cuál es la fórmula para obtener el volumen de un cono de altura h y radio r?
Un cono tiene el doble de altura que un cilindro. Si los radios de sus bases miden igual, ¿cuántas veces es mayor el volumen de un cuerpo que el del otro?
Un cono tiene una altura de 12 cm y un radio de 6 cm. ¿Cuál debe ser el radio de un cilindro con la misma altura para que tengan el mismo volumen?
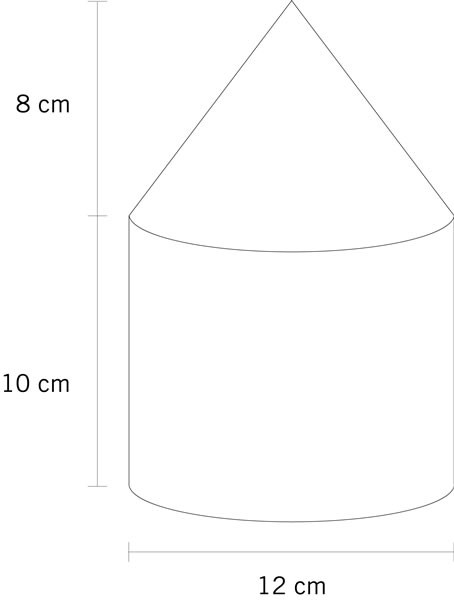
¿Cuál es el volumen del siguiente cuerpo?
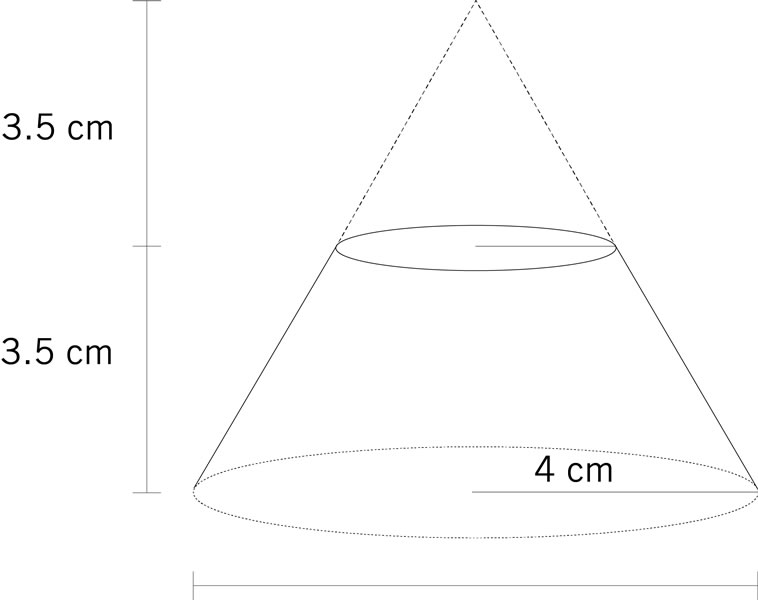
¿Cuál es el volumen de este cono truncado?
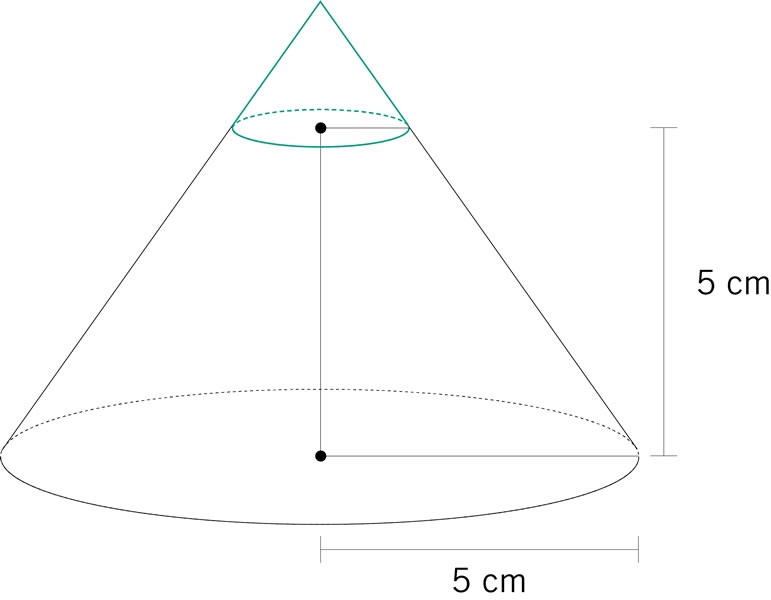
¿Cuál es la capacidad de tres silos iguales si cada uno tiene la forma y las medidas que señala la figura siguiente?
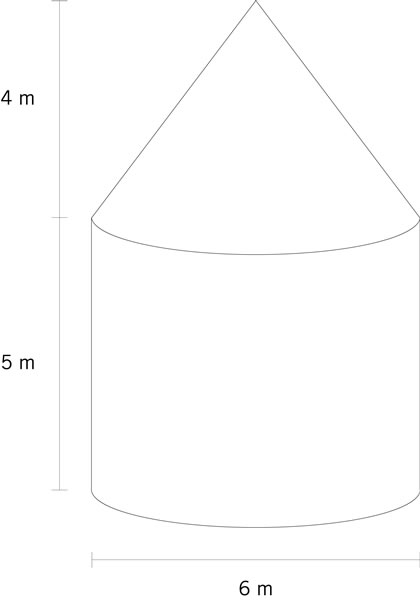
Mariana tiene 2 400 cm3 de cera para hacer velas. ¿Cuántas velas puede hacer si deben tener la forma completa de la figura siguiente?
Las ganancias mensuales de una empresa son iguales a un décimo del cuadrado del capital invertido menos tres veces el capital invertido menos $200.00. ¿Cuál de las siguientes expresiones algebraicas no representa la situación descrita?
¿Cuál de estas gráficas representa el cambio en el área de un rectángulo conforme su base se modifica si, además, ésta es cinco veces más grande que su altura?
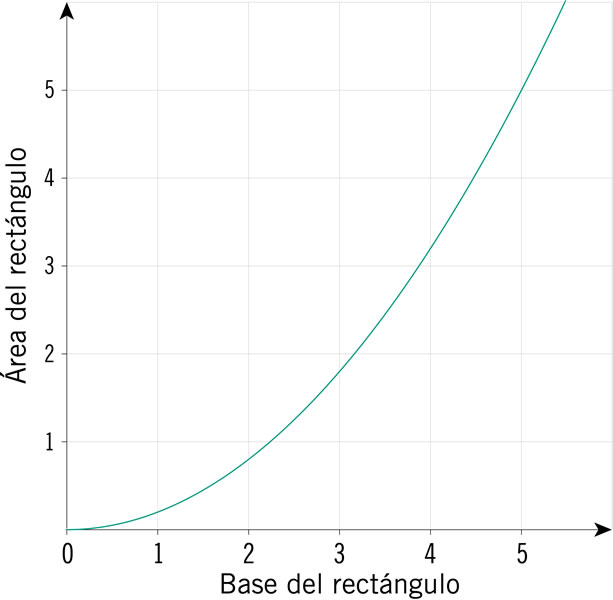
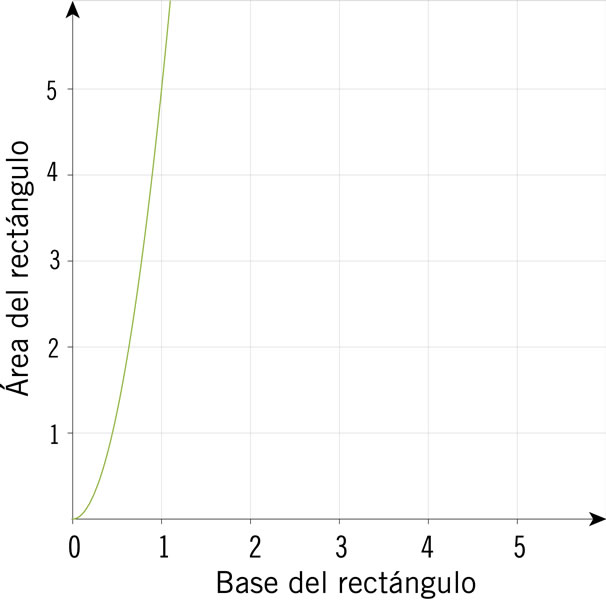
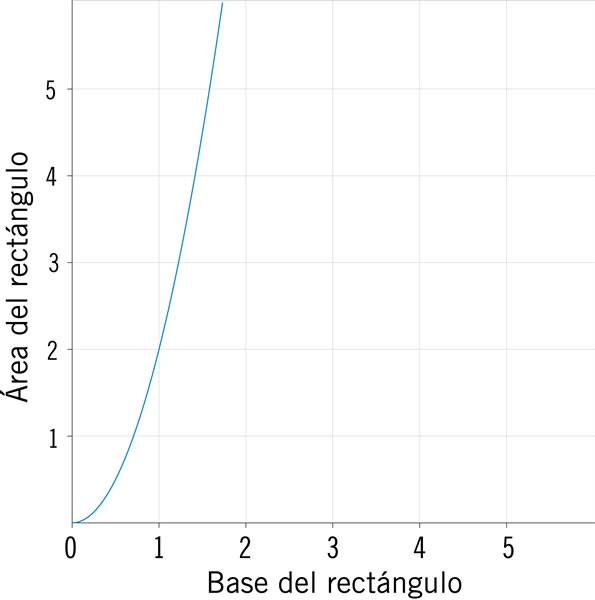
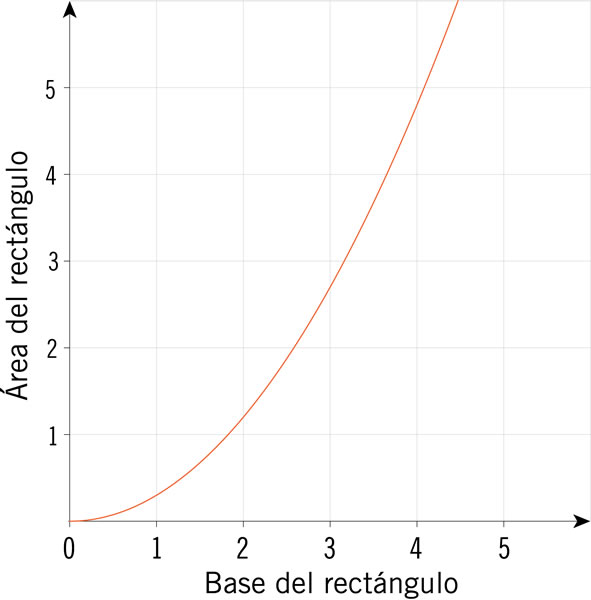
¿En qué sistema cartesiano se muestran las gráficas que representan las expresiones algebraicas y = 3x − 2.5 y y = 2x2 + x − 2?
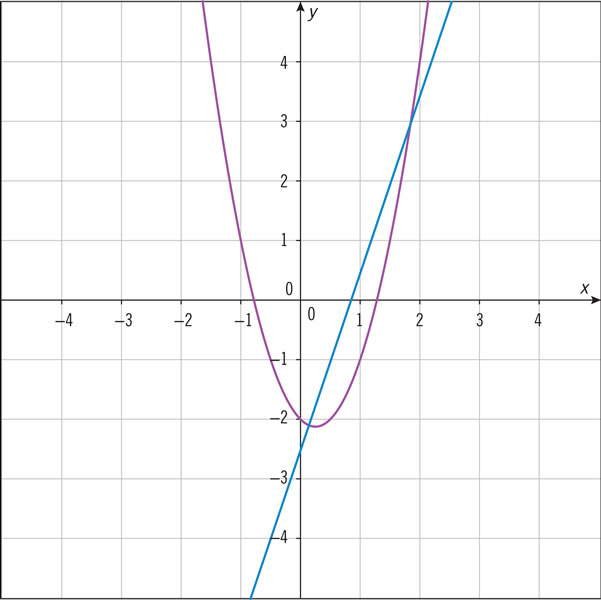
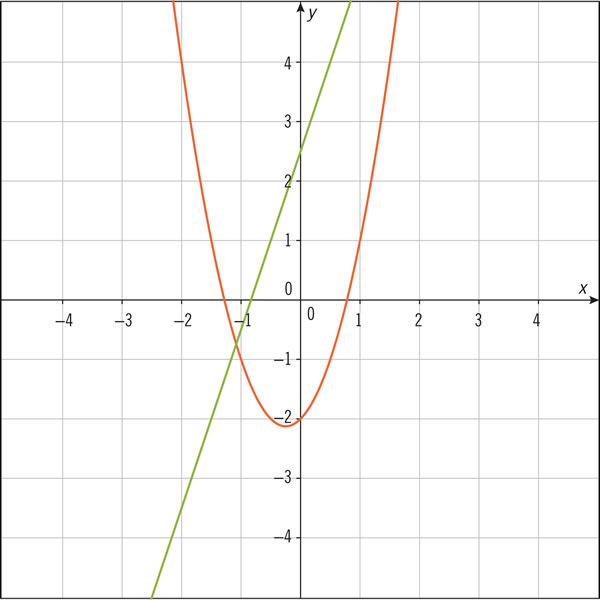
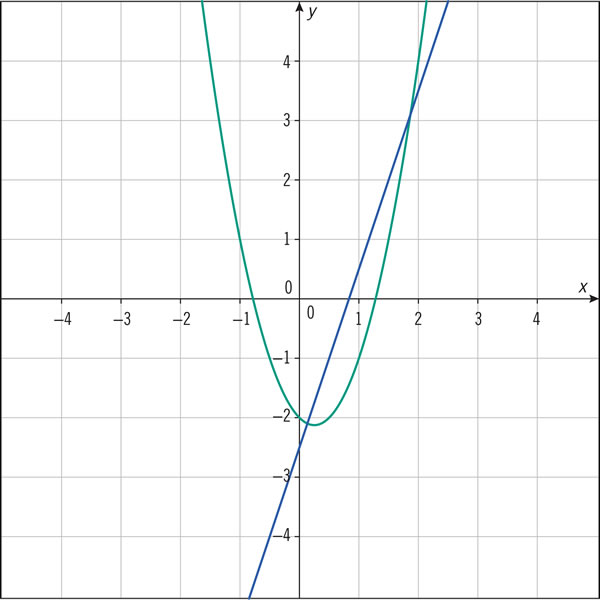
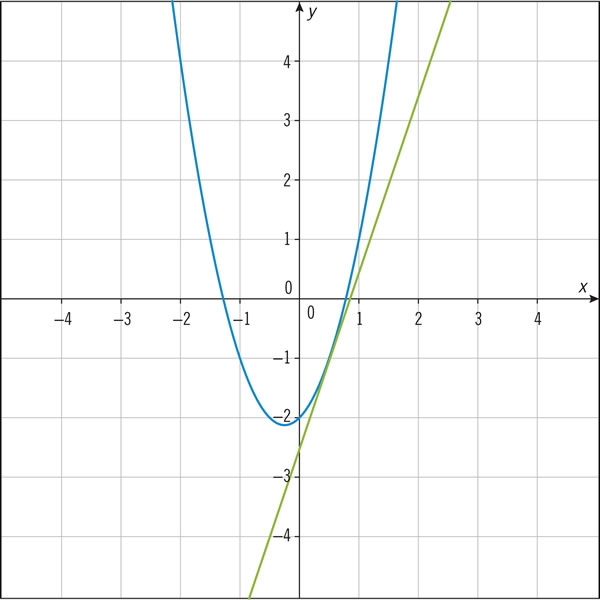
¿Qué expresiones algebraicas corresponden a las siguientes gráficas?
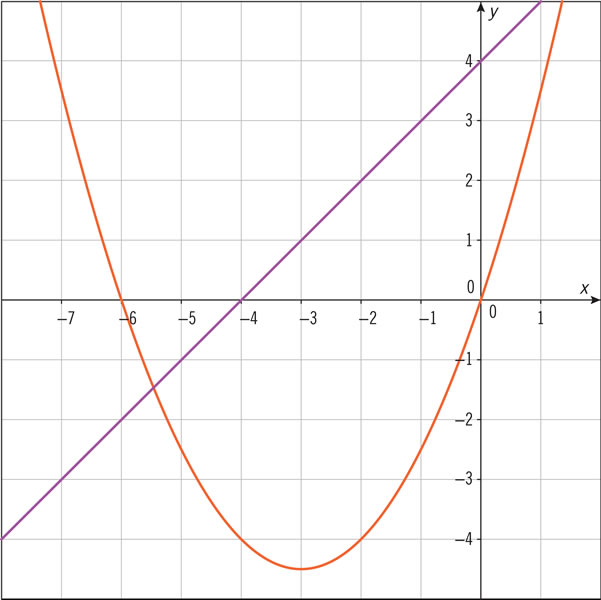
Ricardo y Gonzalo realizan varios juegos. Determina cuál de ellos no es justo.
En una ruleta, dividida en 10 secciones iguales, cada participante apuesta la cantidad de fichas que desee y recibe lo que la ruleta indica cuando se detiene: 3 secciones dicen "El jugador pierde todo", 3 secciones dicen "El jugador pierde la mitad", 2 secciones dicen "El jugador gana una y media veces lo apostado", 2 secciones dicen "El jugador gana el doble". ¿Se trata de un juego justo?
Hilda y Sandra juegan a lanzar dos dados cada uno con las caras numeradas del 1 al 6, y cuando caen, suman los puntos de las caras superiores. Si la suma es 8 o un número menor, Hilda gana un punto y si la suma es 9 o un número mayor, entonces el punto es para Sandra. ¿Con cuál de las siguientes modificaciones a las reglas el juego sería justo? Los cambios no mencionados se conservan.
La base de un triángulo mide 5 unidades y su altura mide a unidades. Además, su área es igual al área de un cuadrado cuyo lado también mide a unidades. ¿Cuál es el valor de a?
Érick entre ayer y hoy dio 13 vueltas al parque. En cada vuelta de ayer se tardó 2 min y en cada vuelta de hoy, 3 min. Además, entre ayer y hoy corrió en total 34 min. ¿Cuántas vueltas, respectivamente, dio ayer y cuántas hoy?
Si se hace un corte paralelo a la generatriz de un cono, ¿cómo se llama la sección cónica resultante?
La altura de un cono es de 7 cm y su radio de 2 cm. Si se le hace una corte paralelo a su base a una altura de 5 cm, ¿cuánto mide el radio del cono más pequeño que se formó?
¿Cómo se calcula el volumen de un cono?
¿Cuál de los siguientes volúmenes se aproxima más al volumen de un cono de 30 cm de altura que tiene una base de 10 cm de diámetro?
El radio de la base de un cilindro mide 5 cm y su altura, 13 cm. Si su volumen es igual al de un cono que tiene una base de 8 cm de radio, ¿cuál es la altura del cono?
¿Entre cuál par de conjuntos existe una relación de variación lineal?
Un juego en el que participan 5 jugadores es justo si...
En una bolsa hay papeles numerados del 1 al 15. Si se extrae un papel y el resultado es un número par mayor que 6 entonces gana Norma; si el resultado es un número menor que 5, gana Víctor. ¿Con cuáles resultados debe ganar Óscar, un tercer participante, para que el juego sea justo?